Kurssin lopputyössäni tarkastelen, miten Bayes-päätösanalyysia voidaan hyödyntää Vantaanjoen taimeniin kohdistuvien arvojen ja tavoitteiden arvioimisessa. Työssä pohditaan myös sidosryhmien osallistamisen tärkeyttä päätöksenteossa.
Työn löydät täältä:
BUGS ei ole ainoa tapaa harjoittaa markov chain monte carlo simulointia, johon bugsin numeerinen laskenta perustuu. R-ohjelmistosta lötyy esimerkiksi paketti rcppbugs, jonka avulla voidaan mcmc simulointi suorittaa pelkästään R-ympäristössä. R on myös sen verran monipuolinen ohjelmointikieli, että simulointi voitaisiin myös koodata sen avulla kokonaan alusta alkaen.
Pelkän R-ohjelmiston käytöstä on tiettyjä etuja. R-ohjelmistoon on saatavilla esimerkiksi shiny-lisäosa, joka mahdollistaa helpon web-appien kehityksen. Kalamallista löytyykin nyt toistaiseksi julkaisematon web-appina toteutettu versio, jonka voi nyt ajaa R-ohjelmiston kautta.
Tämän version laskentatulokset ovat toistaiseksi epäluotettavia ja simuloinnin koodaus saatetaan vielä uudistaa myöhemmin. Web-appi kuitenkin mahdollistaa esimerkiksi helpon priorijakaumien kuvaajien kanssa leikkimisen.
Projektin koodit löytyvät GitHubista ja “Smolt” nimisen appin voi käynnistää R-ohjelmiston kautta seuraavasti:
if(!require(“shiny”)) {
install.packages(“shiny”)
library(shiny)
}
runGitHub(“Smolt”,”hasiOne”)
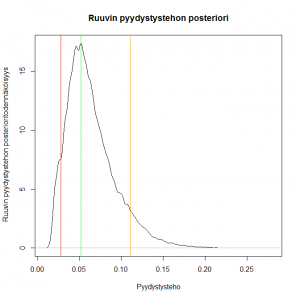
Tämä postaus on jatkoa muutamalle edelliselle postaukselleni, joissa käsittelin pyydystettävyyden mallintamista logistisella regressiomallilla. Ideana ja motivaationa tälle oli se, että käytetyn pyydyksen tehon epäiltiin riippuvan erityisesti veden korkeudesta.
Käsittelin logistista regressiomalli teoreettisesti ja kirjoitin hahmotelmaa siitä, miten malli voitaisiin määritellä BUGS-kielellä. Kuitenkin epäselväksi jäi se, miten prioritieto pyydystettävyydestä saataisiin mukaan malliin. Tämä postaus käsittelee tätä ongelmaa.
Logistinen regressiomalli on muotoa
logit(q) = a + beta[1]*VK +beta[2]*VL + E
VK=veden korkeus, VL=veden lämpötila, E=virhetermi , a= vakiotermi, beta[1] = veden korkeutta vastaava regressiokerroin, beta[2] = veden lämpötilaa vastaava regressiokerroin.
Haluaisimme siis ‘valita’ tämän mallin parametrit niin, että pyydystettävyyden priorijakauma olisi edelleen suurinpiirtein tietty beta-jakauma, kuten aiemminkin. Nyt, koska mallissa pyydystettävyys vaihtelee päivittäin, tarkoittaa tämä oikeastaan sitä, että arvioituna kaikkien päivien yli (tai oikeammin, arvioituna mallin selittäjien jakauman yli), noudattaisi pyydystettävyys haluttua beta-jakaumaa.
Aivan täsmälleen tätä haluttua tulosta emme voi saavuttaa, mutta niin sanotun informatiivisen g-priorin avulla pääsemme hyvin lähelle.
Ratkaistessa todennäköisyys logit-muunnoksesta, saadaan yhtälö
q = exp(x’B) / (1 + exp(x’B) )
jossa X on mallin selittäjät sisältävä matriisi (1, VK, VL) ja B näitä vastaavat kertoimet (a, beta[1], beta[2]).
On näytetty, että jos
B ~ N(b*e, g*n*(X’X)^-1)
ja
x ~ N(u, Z)
missä
b = digamma(a) – digamma(b)
g = [trigamma(a) + trigamma(b)] / p
e = c(1,0,..0) <- p-pituinen vektori
p = parametrien lukumäärä
n = havaintojen lukumäärä
N() = normaalijakauma
x = selittävät muuttujat
niin silloin
exp(x’B) / (1 + exp(x’B) )
vastaa suunnilleen beta-jakaumaa parametrein a ja b.
Tämä siis tarkoittaa, että on mahdollista rakentaa logistinen regressiomalli, jonka priorijakauma vastaa haluttua beta-jakaumaa.
Tämän voi todeta esimerkiksi R-ohjelmiston avulla seuraavasti. Alla olevassa koodissa X on niin kutsuttu design-matrix määriteltynä R-objektina (eli esim matriisi tai data frame, jonka ensimmäinen kolumni on 1, ja toinen ja kolmas esimerkiksi päivittäiset veden korkeudet ja lämpötilat). Koodin ajamiseksi tämä matriisi tulee siis ensin määritellä.
library(MASS)
X <- …
get.bg <- function(alpha, beta, parameters = 3) {
b <- digamma(alpha) – digamma(beta)
g <- trigamma(alpha) + trigamma(beta)
g <- g/parameters
return(c(b = b, g = g))
}
bg <- get.bg(alpha = 3, beta = 50)
Sigma <- bg[[‘g’]]*nrow(X)*solve(t(X) %*% X)
mu <- c(1,0,0)*bg[[‘b’]]
# B noudattaa multinormaalijaumaa, tässä otetaan siitä satunnaisotos
B <- mvrnorm(1000, mu = mu, Sigma = Sigma)
# vektori, jossa todennäköisyyksiä logit-muunnoksesta
p <- apply(B,1,function(bi) {
apply(X,1,function(xi) {
exp(xi%*%bi)/(1+exp(xi%*%bi))
})
})
p <- c(p)
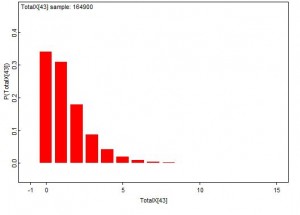
plot(density(p))
Kuvasta nähdään, että tuloksena on haluttu beta(a=3, b=50) jakauma
Viimeisessä henkilökohtaisessa postauksessani kirjoitin pyydystettävyydestä ja sen mallintamisesta. Taimenruuvin pyydystettävyys on tämänhetkisessä mallissa mallinnettu niin, että sen jakauma on riippumaton päivistä. Toisinsanoen ruuvi pyydystää samalla teholla joka päivä.
Esitin viimeksi tälle toisen teoreettisen mahdollisuden; logistinen regressiomalli, jossa päivittäistä pyydystettävyyttä selitetään veden korkeudella ja lämpötilalla.
logit(q) = a + beta[1]*VK +beta[2]*VL + E
VK=veden korkeus, VL=veden lämpötila, E=virhetermi , a= vakiotermi, beta[1] = veden korkeutta vastaava regressiokerroin, beta[2] = veden lämpötilaa vastaava regressiokerroin.
Korkeuden mahdollinen vaikutus on siinä mielessä selkeä, että veden korkeus vaikuttaa havaittavasti pyydyksen toimintaan. Lämpötila taas vaikuttaa taimenten vireyteen, joka saattaa vaikuttaa niiden kykyyn väistää pyydys.
Nyt esimerkiksi veden korkeutta vastaavan regressiokertoimen (b) tulkita on seuraava: Veden korkeuden noustessa yhden yksikön, muuttuu pydystettävyyden logit-muunnos keskimäärin (b) yksikköä silloin, kun veden lämpötila pysyy vakiona.
On eri asia määrittää tilastollinen malli matemaattisesti ja soveltaa kyseistä mallia. Soveltaminen tapahtuu tilastollisella ohjelmistolla, jolla on oma kielensä. Miten logistinen regressiomalli voitaisiin määritellä BUGS-kielellä? Alla on hahmotelma mallista vaihe vaiheelta.
# (1) Oletamme, että logit-muunnos pyydystystodennäköisyydestä (q), (eli log(q / 1- q) ), noudattaa normaalijakaumaa parametrein nyy ja tao. Indeksi d vittaa päivään.
logit_q[d]~dnorm(nyy[d],tao)
# (2) … jakauman odotusarvo on lineaarikombinaatio nyy = a + beta1*VK + beta2*VL
nyy[d] <- alpha + beta1*VK[d] + beta2*VL[d]
# (3) BUGS:ssa normaalijakauman toisena parametrina on varianssin käänteisluku. Varianssi vastaa mallin virhetermiä E. Keskihajonta on yleensä hieman intuitiivisempi tunnusluku hahmottaa, joten priori voidaan määrittää sille ja muunta se varianssin käänteisluvuksi. Voisimme esim olettaa, että emme tiedä virheen suuruudesta juuri mitään.
tao<-pow(E,-2)
E~dunif(0.01,10000)
# (4) mallinnettu logit-muunnos täytyy vielä muuntaa takaisin todennäköisyydeksi. Ratkaistaan siis q yhtälöstä log(q/1-q) = nyy ja käytetään saatua kaavaa. Alla ensin BUGSissa käytettävä tulos ja sen alla myös itse lasku, joka on toistettavissa lukiomatematiikan avuin.
q[d] <- exp(nyy[d]) / (1+exp(nyy[d]))
log(q/1-q) = nyy | exp()
q/1-q = exp(nyy) | *(1-q)
q = exp(nyy) – q*exp(nyy) | + q*e^nyy
q*(1+exp(nyy)) = exp(nyy) | / (1+e^nyy)
q = exp(nyy)/(1+exp(nyy))
# (5) mallin parametreille a, beta1, beta2 tarvitaan vielä priorijakaumat. Alla mallin hahmotelma kokonaisuudessaan ja sen jälkeen muutama huomio ja kehitysidea.
for(d in 1:days) {
logit_q[d]~dnorm(nyy[d],tao)
nyy[d] <- alpha + beta1*WT[d] + beta2*WL[d]
}
tao<-pow(sd,-2)
sd~ dunif(0.01,10000)
a~?
beta1~?
beta2~?
Parametrin a priorijakauma tulisi muodostaa niin, että se huomioi prioritiedon pyydystettävyydestä. Tässä on vielä pohdittavaa.
Lisäksi pitäisi huomioida se, että vaikkakin veden korkeuden nouseminen parantaa pyydystettävyyttä johonkin korkeuteen asti, on oltava sellainen piste, jonka jälkeen pyydystettävyys alkaakin huononemaan. Nimittäin kun veden tilavuus kasvaa niin kalat menevät todennäköisemmin pyydyksestä ohi.
Mallista pitäisikin luultavasti muodostaa polynominen versio, johon lisättäisiin selittäjäksi veden korkeuden neliö. Tällöin malli pystyy muotoutumaan paraabeliksi ja huomioimaan yllämainitun.
Ruuvin pyydystettävyyden prioria mallinnamme binomijakauman konjugaatilla beta -jakaumalla. Valinta on kätevä laskettavuuden lisäksi sisällöllisesti siksi, että täten syntyvässä betabinomimallissa beta-(priori)jakauman parametrit voidaan ymmärtää niin sanottuina ”pseudohavaintoina”. Tämä tarkoittaa, että esimerkiksi alun perin käyttämämme priori Beta (2,8) muuntuu ajatusleikiksi, jossa olisimme saaneet kiinni ennen taimensmolttien muuttoon perustuvan ”varsinaisen” aineiston keruuta 2 kalaa (onnistumista) 10 kokeesta (eli 8 epäonnistumista).
Pseudohavaintopriorimme on perustunut mandariinikokeeseen, jossa on tarkasteltu, kuinka moni eri paikoista jokeen päästetyistä mandariineista on jäänyt ruuviin. Pseudohavaintojen painoarvoa olemme häivyttäneet suhteessa vapautettujen mandariinien todelliseen määrään siten, että lähes kahta sataa mandariinia koskeva aineisto on muunnettu 9 pseudohavainnoksi (1, 8). Tämä kielii mandariinien ja kalojen vertailtavuutta kohtaan tuntemastamme skeptisismistä.
Tämä skeptisyys on näkynyt pseudohavaintojen tarkkuudessa, ei oletuksena mandariinikokeen harhaisuudesta kalojen liikkeiden mallina. Olemme nimittäin määrittäneet pseudohavaintopriorimme siten, että onnistumisten (ruuviin jääneet kalat) ja epäonnistumisten suhde vastaa suoraan mandariinihavaintojen suhteita.
Pseudohavaintopriorimme sisältää siis piilo-oletuksen, jonka perusteella kalat ovat enemmän tai vähemmän kuin mandariinit. Eritoten oletamme, etteivät kalat kykene tietoisesti väistämään rysää tai ruuvia. Nimittäin jos kykenevät, tulisi yleistettäessä mandariinit kaloihin mandariinikokeen todellisten onnistumisten määrää pienentää suhteessa havaittuihin epäonnistumisten määrään.
Kuinka paljon priori sitten vaikuttaa tekemiimme päätelmiin?
Tarkastellaan asiaa kahdella heuristisella tavalla (tähänhän olisi käytössä mm. informaatioteoreettisia tarkkoja mittoja): vertailemalla ruuvin pyydystettävyyden posterioritodennäköisyyden moodia suurimman uskottavuuden estimaattiin sekä posterioritodennäköisyyteen, joka saataisiin, jos mallin rakentamiseen käytettäisiin informatiivisen sijaan maksimaalisen epäinformatiivista Jeffreysin prioria.
Suurimman uskottavuuden estimaatti määräytyy aineiston perusteella. SU -estimoinnissa selvitetään uskottavuusfunktion logiikan mukaisesti, millä parametrin arvolla havaittu aineisto olisi todennäköisin. Jos tässä ”aineisto” ymmärrettäisiin kalojen uudelleenpyyntidatana (jotta vertailu mandariineihin olisi mahdollisimman puhdas), olisi binomikokeen onnistumistodennäköisyyden suurimman uskottavuuden estimaatti yksinkertaisesti kiinniotettujen kalojen suhde kaikista merkatuista kaloista. Uusimmalla aineistolla tämä suhde on ruuvin kohdalla 2/72=1/36=0.0278.
Tällä hetkellä ruuvin pyydystystehon posteriorimme näyttää seuraavalta:
Kuvion punainen viiva näyttää suurimman uskottavuuden estimaatin, vihreä viiva posteriorimoodin ja oranssi priorimoodin paikan. Posteriorimoodimme on ymmärrettävästi suurimman uskottavuuden estimaattia korkeampi, onhan tätä myös priorimme (1/9). Posterioriestimaattimme asettuu SU -estimaatin ja priorimoodin väliin, jonkin verran lähemmäksi ensin kuin viimeksi mainittua.
Käytettäessä Jeffreysin epäinformatiivista prioria Beta (0.5;0.5) sekä ruuville että rysälle, saadaan ruuvin pyydystettävyydelle vain hieman vasemmalle varsinaisesta mallistamme siirtynyt posteriorijakauma.
Käyttämämme pyydystettävyysmallin posteriorin keskiarvo on 0.064 (noin 1/16) ja 95 % luottamusväli (0.022; 0.136). Pyydystettävyyden posteriorin keskiarvo Jeffreysin priorilla on puolestaan 0.055 ja 95 % luottamusväli (0.018; 0.129). Jeffreysin priori nostaa aineiston vaikutusvaltaa ja hilaa täten posterioria kohti suurimman uskottavuuden estimaattia (1/36) ja pois priorimoodista (1/9).
Onko mandariini siis kala? Vaikuttaisi siltä, että informatiivinen beta -priorimme on ”ristiriidassa” havaitun aineiston kanssa ja mandariini ei tämän perusteella vaikuttaisi olevan kala. Todennäköisyys havaita 2 tai vähemmän kalaa 72 kokeella, jos mandariinipseudohavaintomme 1/9 vastaisi todellista pyydystystehoa, on noin 1 % (nollahypoteesin testauksen hirviölogiikalla).
Huomionarvoista on, ettei ero pyydystettävyyden posteriorissa ole kuitenkaan kovin suuri, vaikka siirryttäisiinkin käyttämään epäinformatiivista Jeffreysin prioria (posteriorin keskiarvo siirtyy 1/16 -> 1/18).
Yksi tapa sisällyttää mandariinihavaintojen kalojen priorina käyttämiseen liittyvät epäilyksemme olisi rakentaa hierarkinen malli, jossa myös betapriorin parametrimme noudattaisivat omaa priorijakaumaansa. Tämä olisi oletettavasti perustellumpi ratkaisu haasteeseen kuin Jeffreysin priori. Onhan niin, että mandariinit välittävät jotain tietoa kalojen käyttäytymisestä, vaikka olisikin luonteeltaan harhaista ja epätarkkaa.
Päivä Smoltteja
22.5 0
23.5 2
24.5 0
25.5 0
Päiviteltiin taas hieman mallia viimeisimmällä, joskaan ei niin kovin tuoreella saatikka runsaalla datalla. Smoltittomia päiviä on sattunut tässä jo useampi, joko rupeaa kalat vedestä loppumaan??
Kokonaismäärän N keski- ja hajontalukuja
Arvoi saatiin noin 120 000 iteraatiolla, joista poistettiin 24 000 ensimmäistä ja valittiin joka 15:sta iteraatio konvergoitumisen varmistamiseksi ja autokorrelaation pienentämiseksi. Kuvaajassa näkyvä piikikkyys johtuu arvojen pyöristämisestä mallin sisällä.
Kokonaismäärän N posteriorijakauma
Uusin mallin antama arvio kokonaismäärän todennäköisyysjakauman keskiarvosta on 2272, keskihajonnalla 1181. 95 % todennäköisyysväli löytyy arvojen 582 ja 4975 väliltä. Arvio on siis edelleenkin hyvin varovainen, mutta arviot tarkentuvat kun tieto lisääntyy!
Kurssilla ollaan nyt tilanteessa, jossa mallin rakentamisesta on siirrytty päätöksentekoanalyyseihin. Suurimmalta osin ainakin. Rysän ollessa padon edessä, saadaan kerättyä tietoa, kuinka moni taimen joutuu mahdollisesti turbiinien rattaisiin ja sushina padon alla odottavien kalojen suihin. Tai näin ainakin oli ajatus kurssilaisten mielissä.
Rysä otettiin pois käytöstä jo muutamia päiviä sitten, eikä dataa saatu kerättyä juuri yhtään. Rysä kerkesi olla padon edessä vain kahdeksan päivän ajan. Tänä aikana n. 25 % pyydetyistä kaloista päätyi padon edessä olevaan rysään. Mikäli luku olisi sama myös todellisuudessa, olisi merelle vaeltavilla taimenilla suuri mahdollisuus päättää vaelluksensa tähän esteeseen.
Padon purkamisen päätöksentekoanalyysia rakentaessamme törmäsin itse monesti ongelmaan, jossa osa osioista tuli ehkä ylimietittyäkin, tämän johtaen hyvin yksityiskohtaiseen ongelman tarkasteluun, osan taas jäädessä hyvin yleiselle tasolle. Jotta päätöksenteko ”kartta” olisi toimiva, pitäisi kaikki kohteet saada suunnilleen samalle tarkastelutasolle.?!
Toinen ongelma muodostui hyödyn (utility) ajattelusta. Analyysissä pitäisi pystyä arvottamaan kartan eri osiot erilaisilla hyödyillä tai vaihtoehtoisesti haitoilla. Jotta tämä onnistuisi, pitäisi mallissa pystyä jotenkin valitsemaan vaalikonemaisesti näkeekö asiat hyötyinä vai haittoina ja antamaan näille, erilaisia painoarvoja.
Päivä: 42
Pyydettyjä taimenen smoltteja kaiken kaikkiaan: 70
Merkattuja taimenen smoltteja kaiken kaikkiaan: 70
Uudelleen pyydettyjä taimenen smoltteja kaiken kaikkiaan: 2
Vähän pienempien ja suurempien teknisten ongelmien jälkeen valmistui päivän 42 (21.5.) tulokset. Tässä mallissa olemme päivittäneen pyydystettävyyden prioria, koska pyydystettävyyttä testaava mandariinikoe uusittiin. Kuten myös edellisessä tulospostauksessa, kaikki seuraavat tulokset perustuvat yli neljän mallimme keskiarvostettuihin posterioriestimaatteihin.
Malli tuottaa lähtemisintensiteetille totaaliestimaatin (Kuva 1), jossa 95 % todennäköisyydellä vaeltavien taimensmolttien kokonaismäärä on välillä 483–5035 (Taulukko 1). Todennäköisin yksittäinen arvio kokonaismäärästä on 500 ja 1500 välissä.
Kuva 1. Posteriorijakauma vaeltavien taimensmolttien kokonaismäärästä 2015.
Perjantaina 22.5. vaeltavien taimensmolttien lukumäärä (n[43]) on 95% todennäköisyydellä välillä 3–81 (Taulukko 1). Todennäköisin yksittäinen arvio vaeltavien smolttien lukumäärästä on 9 (Kuva 2).
Kuva 2. Posteriorijakauma vaeltavien taimensmolttien määrästä perjantaina 22.5.2015.
Perjantaina 22.5. pyydyksiin jäävien taimensmolttien lukumäärä (x[26]) on 95% todennäköisyydellä välillä 0–5 (Taulukko 1). Jälleen kerran todennäköisin yksittäinen arvio on, että pyydyksiin ei jää yhtään taimensmolttia (Kuva 3).
Edellisellä kurssikerralla puhuimme toisen pyydyksen (rysän) uuden sijainnin huomioimisesta mallissa. Aihetta on käsitelty myös aiemmin blogissa, mutta ehdotusta ei ole huomioitu vielä tässä mallissa.
Kuva 3. Posteriorijakauma pyydyksiin jäävien taimensmolttien määrästä perjantaina 22.5.2015.
Taulukko 1. Parametrien N, n[26] ja TotalX[26] posteriorijakaumien tunnusluvut.
| mean | sd | MC_error | val2.5pc | median | val97.5pc | start | sample | |
| N | 1985.0 | 1212.0 | 35.16 | 483.0 | 1694.0 | 5035.0 | 51 | 164900 |
| n[43] | 25.76 | 20.81 | 0.5681 | 3.0 | 20.0 | 81.0 | 51 | 164900 |
| TotalX[43] | 1.363 | 1.66 | 0.02455 | 0.0 | 1.0 | 5.0 | 51 | 164900 |
Minkä muotoisen käppyrän, suoran tai niin edespäin sovittaisit seuraavaan aineistoon?
Pisteet kuvaavat päivittäisiä kiinnijääneitä taimenen smoltteja päivään 38 asti.
Mielestäni prima facie ja äkkiseltään kohtalaiselta sovitteelta vaikuttaisi horisontaalinen suora, joka kulkisi noin yhdessä päivittäisessä havainnossa yli kaikkien seuranta-ajanjakson päivien.
Mitään trendiä on nimittäin ainakin minun mielestäni kuviosta kovin vaikea havaita. Herkällä tulkinnalla voitaisiin kenties todeta havaintojen hieman lisääntyneen päivien kuluessa. Tällöin horisontaalisen sijaan varovaisesti nouseva suora saattaisi toimia.
Entä onko kuviossa useamman havainnon muodostamia havaintohuippuja (useamman siksi, että näissä olisi tulkittavissa jotain systematiikkaa)? Edes tällaisia on mielestäni vaikea päätellä kuviossa esiintyvän: ehkä korkeintaan päivinä 20, 21 ja 22, kenties jälleen päivinä 36,37 ja 38.
Onko näissä päivissä jotain muuta erityistä, kuin mitä mallien teoriapohjalta voitaisiin ennustaa? No, rysä on ollut yhdessä ruuvin kanssa toiminnassa kaiken kaikkiaan päivinä 16-21 ja 35-38. Kun tämän huomioi, vaikuttaisi hajontakuvioon sopivan erityisen hyvin mainittu horisontaalinen suora, josta muutamat rysän vaikutuksen poistamisen jälkeen jäljelle jäävät poikkeavat havainnot (outlierit), ovat suurusluokkaa 3-4, eivätkä siksi kovin epätodennäköisiä ehdolla horistontaalinen sovite.
Tällainen “horisontaalinen sovite” sopisi yhteen muuttointensiteetin mallin tasajakauma kanssa. Havaintommehan oletetaan tulevan (muuten paitsi pyydysten määrältä) yli päivien vakiolla pyydystettävyysteholla, tietyn mutta tuntemattoman kokoisesta smolttipopulaatiosta, yli päivien mallinnetuilla muuttointensiteeteillä. Siispä ennustettu muuttointensiteetti määrittää yhdessä pyydysten määrän kanssa suurimman osan siitä, minkä “muodon” oletamme hajontakuviossa esiintyvän.
Mielenkiintoisen poikkeuksen tähän tekee totaaliestimaattimme. Jos havaintomäärät “raahaavat perässä” totaaliprioria, tulee mallin kyetä ennustamaan havaintopiikkejä tai systemaattisesti lisääntyviä havaintoja jäljellä oleville seuranta-ajanjakson päiville. Tasajakauma ei tähän juuri kykene.
Mutta selittääkö tämä sen, että tasajakauma saa mallivertailussamme (https://blogs.helsinki.fi/taimenlaskenta/?p=221) posterioritodennäköisyydekseen 0? Lähes varmoina tulosten perusteella pidettävät (joko tai) normaalijakauma ja lognormaalijakauma eivät vaikuttaisi sopivan aineistoon yhtään tasajakaumaa paremmin. Tekisi mieli sanoa päinvastoin.
No, asia ei ole näin yksinkertainen. Mallia ei tule suosia vain datan perusteella, minkä vuoksi postauksen aloittama kysymys on ikään kuin nurinkurinen. Pitäisi pohtia, mikä priorikäsityksen mukaan perusteltu malli on myös perusteltu ehdolla aineisto. Mallien posterioreihin vaikuttavatkin niiden uskottavuuden lisäksi sekä mallien parametrien määrä, parametrien priorit että mallien priorit.
Koska viimeksi mainitut ovat meillä kategorisesti tasan (pun intended) eli 1/4, eivät erot mallien posterioreissa voi tästä johtua. Siispä ne vaikuttaisivat johtuvan ennen kaikkea mallien parametreista ja näiden prioreista.
Muissa malleissa on enemmän parametreja kuin tasajakaumassa, jossa muuttointensiteetin määrittää 1/60 jokaisena päivänä. Useammalla parametrilla voidaan paremmin myötäillä saatua dataa. Sopivilla parametrien prioreilla voitaneen mallista saada tasajakaumaa selvästi joustavampi ja vielä kun käy niin, että havaintopiikki osuu ennalta määrättyyn priorikohtaan normaalijakaumaa, voidaan juuri kyseinen piikki selittää erinomaisesti jakauman joustavalla muodolla. Mutta mitä tapahtuu, jos ja kun “piikkejä” tulee useampia ja ne ovat vain yhden päivän mittaisia?
Ja eikö parametrien määrästä pitäisi rankaista? Eikö hyvä malli ole SEKÄ sopiva aineistoon (goodness of fit) että yksinkertainen (parsimonious)? Tällöin tasajakauma tuntuisi edellisen kuvion ja yksinkertaisuudensa vuoksi vähintään intuitiivisesti hyvältä valinnalta.
Mutta. Teoriapohjalta varmasti tiedetään, ettei tasajakauma voi olla oikea malli. Smoltit eivät muuta tasaista virtaa. Jos ja kun näin on, tulisi tämän näkyä mallivalintojen prioreissa ja vaikuttaa pääasiassa sitä eikä muuta kautta malliemme posterioritodennäköisyyksiin.
Tänään tuli puheeksi rysän uusi sijainti ja sen huomioiminen mallin sisällä. Rysä on aikaisemmin sijainnut joen haarautumiskohdassa ja on nyttemmin (13.5.) siirretty joen länsihaaran puolelle, hieman haarautumiskohdan yläpuolelle.
Saimme myös uutta mandariinikoetietoa, jonka mukaan nyt kaikkien kolmen kokeen aikana “vapautetusta” 188 mandariineista 139 on päätynyt joen länsihaaraan. Olemme käyttäneet tätä estimaattina smolttien vaeltamisesta, joten voisimme myös olettaa rysän pyytävän nyt tehokkaammin sen ollessa voimakkaimmin virtaavassa paikassa.
Hahmottelin helpohkon pikaratkaisun ongelmalle, jossa uutta rysää lähdetään yksinkertaisesti arvoimaan kokonaan uudella priorijakaumalla. Tämä ratkaisu ei edellyttäisi suuria muutoksia malliin:
Fyke_q[d]<-q_F*Fyke_op[d]*step(32-d)+q_F2*Screw_op[d]*step(d-32)
q_F2~dbeta(1,3)
Step-funktiot palauttavat yksinkertaisesti nollan erotuksen ollessa <0, jolloin summattava saa arvon nolla. Siis päivillä 1-32 käytetään rysän aiempaa priorijakaumaa q_F ja 32-60 uutta q_F2:ta. q_F2:lle annettu arvio hieman suuremmasta pyyntitehosta.
Tämä ratkaisu ei välttämättä ole ongelmaton. Rysän pyydystävyys päivittyy mielestäni datalla samaan tapaan kuin aikasemminkin. Se tarkoittaa, että kaikki rysän aikasemmassa paikassa sijaitessaan keräämä data pyydystettävyydestä siirtyy nyt “uudelle rysälle”, eli uudelle sijainnille. Tämä on mielestäni ristiriitaista sen kanssa, että rysän uuteen sijaintiin perustuva priori antaa nimenomaan ymmärtää, ettei sen pyydystävyys ole vain sen ominaisuus vaan riippuvainen myös sen sijannista. Tähän on syytä paneutua lisää ja katsoa miten tarkalleen riippuvuudet kulkevat pyydystävyys-mallin sisällä.