Ruuvin pyydystettävyyden prioria mallinnamme binomijakauman konjugaatilla beta -jakaumalla. Valinta on kätevä laskettavuuden lisäksi sisällöllisesti siksi, että täten syntyvässä betabinomimallissa beta-(priori)jakauman parametrit voidaan ymmärtää niin sanottuina ”pseudohavaintoina”. Tämä tarkoittaa, että esimerkiksi alun perin käyttämämme priori Beta (2,8) muuntuu ajatusleikiksi, jossa olisimme saaneet kiinni ennen taimensmolttien muuttoon perustuvan ”varsinaisen” aineiston keruuta 2 kalaa (onnistumista) 10 kokeesta (eli 8 epäonnistumista).

 
Pseudohavaintopriorimme on perustunut mandariinikokeeseen, jossa on tarkasteltu, kuinka moni eri paikoista jokeen päästetyistä mandariineista on jäänyt ruuviin. Pseudohavaintojen painoarvoa olemme häivyttäneet suhteessa vapautettujen mandariinien todelliseen määrään siten, että lähes kahta sataa mandariinia koskeva aineisto on muunnettu 9 pseudohavainnoksi (1, 8). Tämä kielii mandariinien ja kalojen vertailtavuutta kohtaan tuntemastamme skeptisismistä.

 
Tämä skeptisyys on näkynyt pseudohavaintojen tarkkuudessa, ei oletuksena mandariinikokeen harhaisuudesta kalojen liikkeiden mallina. Olemme nimittäin määrittäneet pseudohavaintopriorimme siten, että onnistumisten (ruuviin jääneet kalat) ja epäonnistumisten suhde vastaa suoraan mandariinihavaintojen suhteita.

 
Pseudohavaintopriorimme sisältää siis piilo-oletuksen, jonka perusteella kalat ovat enemmän tai vähemmän kuin mandariinit. Eritoten oletamme, etteivät kalat kykene tietoisesti väistämään rysää tai ruuvia. Nimittäin jos kykenevät, tulisi yleistettäessä mandariinit kaloihin mandariinikokeen todellisten onnistumisten määrää pienentää suhteessa havaittuihin epäonnistumisten määrään.

Kuinka paljon priori sitten vaikuttaa tekemiimme päätelmiin?
Tarkastellaan asiaa kahdella heuristisella tavalla (tähänhän olisi käytössä mm. informaatioteoreettisia tarkkoja mittoja): vertailemalla ruuvin pyydystettävyyden posterioritodennäköisyyden moodia suurimman uskottavuuden estimaattiin sekä posterioritodennäköisyyteen, joka saataisiin, jos mallin rakentamiseen käytettäisiin informatiivisen sijaan maksimaalisen epäinformatiivista Jeffreysin prioria.

 
Suurimman uskottavuuden estimaatti määräytyy aineiston perusteella. SU -estimoinnissa selvitetään uskottavuusfunktion logiikan mukaisesti, millä parametrin arvolla havaittu aineisto olisi todennäköisin. Jos tässä ”aineisto” ymmärrettäisiin kalojen uudelleenpyyntidatana (jotta vertailu mandariineihin olisi mahdollisimman puhdas), olisi binomikokeen onnistumistodennäköisyyden suurimman uskottavuuden estimaatti yksinkertaisesti kiinniotettujen kalojen suhde kaikista merkatuista kaloista. Uusimmalla aineistolla tämä suhde on ruuvin kohdalla 2/72=1/36=0.0278.

 
Tällä hetkellä ruuvin pyydystystehon posteriorimme näyttää seuraavalta:

Kuvion punainen viiva näyttää suurimman uskottavuuden estimaatin, vihreä viiva posteriorimoodin ja oranssi  priorimoodin paikan. Posteriorimoodimme on ymmärrettävästi suurimman uskottavuuden estimaattia korkeampi, onhan tätä myös priorimme (1/9). Posterioriestimaattimme asettuu SU -estimaatin ja priorimoodin väliin, jonkin verran lähemmäksi ensin kuin viimeksi mainittua.

Käytettäessä Jeffreysin epäinformatiivista prioria Beta (0.5;0.5) sekä ruuville että rysälle, saadaan ruuvin pyydystettävyydelle vain hieman vasemmalle varsinaisesta mallistamme siirtynyt posteriorijakauma.

Käyttämämme pyydystettävyysmallin posteriorin keskiarvo on 0.064 (noin 1/16) ja 95 % luottamusväli (0.022; 0.136). Pyydystettävyyden posteriorin keskiarvo Jeffreysin priorilla on puolestaan 0.055 ja 95 % luottamusväli (0.018; 0.129). Jeffreysin priori nostaa aineiston vaikutusvaltaa ja hilaa täten posterioria kohti suurimman uskottavuuden estimaattia (1/36) ja pois priorimoodista (1/9).

Onko mandariini siis kala? Vaikuttaisi siltä, että informatiivinen beta -priorimme on ”ristiriidassa” havaitun aineiston kanssa ja mandariini ei tämän perusteella vaikuttaisi olevan kala. Todennäköisyys havaita 2 tai vähemmän kalaa 72 kokeella, jos mandariinipseudohavaintomme 1/9 vastaisi todellista pyydystystehoa, on noin 1 % (nollahypoteesin testauksen hirviölogiikalla).
Huomionarvoista on, ettei ero pyydystettävyyden posteriorissa ole kuitenkaan kovin suuri, vaikka siirryttäisiinkin käyttämään epäinformatiivista Jeffreysin prioria (posteriorin keskiarvo siirtyy 1/16 -> 1/18).

Yksi tapa sisällyttää mandariinihavaintojen kalojen priorina käyttämiseen liittyvät epäilyksemme olisi rakentaa hierarkinen malli, jossa myös betapriorin parametrimme noudattaisivat omaa priorijakaumaansa. Tämä olisi oletettavasti perustellumpi ratkaisu haasteeseen kuin Jeffreysin priori. Onhan niin, että mandariinit välittävät jotain tietoa kalojen käyttäytymisestä, vaikka olisikin luonteeltaan harhaista ja epätarkkaa.

Minkä muotoisen käppyrän, suoran tai niin edespäin sovittaisit seuraavaan aineistoon?

Pisteet kuvaavat päivittäisiä kiinnijääneitä taimenen smoltteja päivään 38 asti.

Mielestäni prima facie ja äkkiseltään kohtalaiselta sovitteelta vaikuttaisi horisontaalinen suora, joka kulkisi noin yhdessä päivittäisessä havainnossa yli kaikkien seuranta-ajanjakson päivien.

Mitään trendiä on nimittäin ainakin minun mielestäni kuviosta kovin vaikea havaita. Herkällä tulkinnalla voitaisiin kenties todeta havaintojen hieman lisääntyneen päivien kuluessa. Tällöin horisontaalisen sijaan varovaisesti nouseva suora saattaisi toimia.

Entä onko kuviossa useamman havainnon muodostamia havaintohuippuja (useamman siksi, että näissä olisi tulkittavissa jotain systematiikkaa)? Edes tällaisia on mielestäni vaikea päätellä kuviossa esiintyvän: ehkä korkeintaan päivinä 20, 21 ja 22, kenties jälleen päivinä 36,37 ja 38.

Onko näissä päivissä jotain muuta erityistä, kuin mitä mallien teoriapohjalta voitaisiin ennustaa? No, rysä on ollut yhdessä ruuvin kanssa toiminnassa kaiken kaikkiaan päivinä 16-21 ja 35-38. Kun tämän huomioi, vaikuttaisi hajontakuvioon sopivan erityisen hyvin mainittu horisontaalinen suora, josta muutamat rysän vaikutuksen poistamisen jälkeen jäljelle jäävät poikkeavat havainnot (outlierit), ovat suurusluokkaa 3-4, eivätkä siksi kovin epätodennäköisiä ehdolla horistontaalinen sovite.

Tällainen “horisontaalinen sovite” sopisi yhteen muuttointensiteetin mallin tasajakauma kanssa. Havaintommehan oletetaan tulevan (muuten paitsi pyydysten määrältä) yli päivien vakiolla pyydystettävyysteholla, tietyn mutta  tuntemattoman kokoisesta smolttipopulaatiosta, yli päivien mallinnetuilla muuttointensiteeteillä. Siispä ennustettu muuttointensiteetti määrittää yhdessä pyydysten määrän kanssa suurimman osan siitä, minkä “muodon” oletamme hajontakuviossa esiintyvän.

Mielenkiintoisen poikkeuksen tähän tekee totaaliestimaattimme. Jos havaintomäärät “raahaavat perässä” totaaliprioria, tulee mallin kyetä ennustamaan havaintopiikkejä tai systemaattisesti lisääntyviä havaintoja jäljellä oleville seuranta-ajanjakson päiville. Tasajakauma ei tähän juuri kykene.

Mutta selittääkö tämä sen, että tasajakauma saa mallivertailussamme (https://blogs.helsinki.fi/taimenlaskenta/?p=221) posterioritodennäköisyydekseen 0? Lähes varmoina tulosten perusteella pidettävät (joko tai) normaalijakauma ja lognormaalijakauma eivät vaikuttaisi sopivan aineistoon yhtään tasajakaumaa paremmin. Tekisi mieli sanoa päinvastoin.

No, asia ei ole näin yksinkertainen. Mallia ei tule suosia vain datan perusteella, minkä vuoksi postauksen aloittama kysymys on ikään kuin nurinkurinen. Pitäisi pohtia, mikä priorikäsityksen mukaan perusteltu malli on myös perusteltu ehdolla aineisto. Mallien posterioreihin vaikuttavatkin niiden uskottavuuden lisäksi sekä mallien parametrien määrä, parametrien priorit että mallien priorit.

Koska viimeksi mainitut ovat meillä kategorisesti tasan (pun intended) eli 1/4, eivät erot mallien posterioreissa voi tästä johtua. Siispä ne vaikuttaisivat johtuvan ennen kaikkea mallien parametreista ja näiden prioreista.

Muissa malleissa on enemmän parametreja kuin tasajakaumassa, jossa muuttointensiteetin määrittää 1/60 jokaisena päivänä. Useammalla parametrilla voidaan paremmin myötäillä saatua dataa. Sopivilla parametrien prioreilla voitaneen mallista saada tasajakaumaa selvästi joustavampi ja vielä kun käy niin, että havaintopiikki osuu ennalta määrättyyn priorikohtaan normaalijakaumaa, voidaan juuri kyseinen piikki selittää erinomaisesti jakauman joustavalla muodolla. Mutta mitä tapahtuu, jos ja kun “piikkejä” tulee useampia ja ne ovat vain yhden päivän mittaisia?

Ja eikö parametrien määrästä pitäisi rankaista? Eikö hyvä malli ole SEKÄ sopiva aineistoon (goodness of fit) että yksinkertainen (parsimonious)? Tällöin tasajakauma tuntuisi edellisen kuvion ja yksinkertaisuudensa vuoksi vähintään intuitiivisesti hyvältä valinnalta.

Mutta. Teoriapohjalta varmasti tiedetään, ettei tasajakauma voi olla oikea malli. Smoltit eivät muuta tasaista virtaa. Jos ja kun näin on, tulisi tämän näkyä mallivalintojen prioreissa ja vaikuttaa pääasiassa sitä eikä muuta kautta malliemme posterioritodennäköisyyksiin.

Pyydettyjä smoltteja on tällä hetkellä vain 60 kappaletta vaikka oletettu vaellus mereen piti asiantuntija tiedon mukaan käynnistyä vedenlämpötilan saavuttaessa 8 astetta. Ympäristö.fi sivuilta katsottaessa vesi on tällä hetkellä Pirttinrannan mittauspisteessä jo 11 asteessa. Lämpötilan nousu olisi siis pitänyt jo näkyä pyydyksissä, suurimpina saalismäärinä. Tällä hetkellä mitään piikkiä ei ole havaittavissa, vaan pyydettyjen smolttien määrä vaihtelee satunnaisesti 1 – 6 smoltin välillä, vaikka pyydysten määrä on tuplattu. Alkujaanhan pyydyksenä toimi vain joensivuhaarassa oleva ruuvi. Nykyään käytössä on myös rysä. Toisen pyydyksen lisääminen luulisi jotenkin näkyvän pyydettyjen smolttien määrässä.

Vanhassa mallissamme päivitimme pyydysten ”tehoa” sitä mukaan kun kaloja saatiin pyydyksiin. Pyydetty kala oli ensin failure ja sitten succes mikäli merkattu kala saatiin pyydettyä uudestaan. Priorit saatiin malliin Vesi- ja Kalatutkimus Oy:n mandariinikokeesta. Mandariini kokeessa mandariineista pyydykseen päätyi 20 %. Jos mandariineja ajateltaisiin merkattuina smoltteina, olisi uudelleenpyydettävyys riittävällä tasolla, jotta voitaisiin arvioida smolttien kokonaismäärää luotettavasti. Tällä hetkellä uudelleen pyydettyjä kaloja on vasta 1, joten kahdella pyydyksellä päästään vain 1,7 % uudelleenpyydettävyyteen. Kurssilla oli tosin puhetta, että smoltit saattavat kuitenkin tulla pyydykseen uudestaan vasta 1-2 viikon päästä siitä, kun ne on edellisen kerran saatu pyydettyä. Pyydykset ovat nyt kuitenkin pyytäneet jo 40 päivän ajan, joten viiveen ei enää pitäisi vaikuttaa siihen, että merkattuja kaloja ei onnistuta pyytämään takaisin. Tällä hetkellä vanhan mallin pyydysteho olisi niin alhaalla, että en tiedä olisiko sillä voinut antaa luotettavaa arvioita vaelluskannan koosta.

Itseäni on myös ihmetyttänyt pyydysten sijoittaminen. Jo kokeen alkaessa puhuttiin, että ruuvi ei toimi kunnolla, koska virtaus on niin pieni, että ruuvi ei pyöri kunnolla. Sitten rysä asetettiin aluksi joen haaraumaan. Ymmärtääkseni pyydykset toimivat sitä paremmin mitä kovempi virtaus on. Tällöin smolttien on vaikeampi välttää ”omituista kapistusta”. Tästä syystä pyydys tulisi sijoittaa joen ”päävirran” kohdalle. Toki pyydysten sijoittamiseen on vaikuttanut moni asia, ja juurikin kovasta virrasta johtuen sitä, ei ehkä ole voitu sijoittaa juuri sinne minne se olisi haluttu.

Uudessa mallissamme otimme mallia kurssinvetäjämme pyydysmallista ja siinäkin pyydysten teho päivittyy ymmärtääkseni samaan tapaan, kuin vanhassakin mallissa, näin ainakin teoriassa. Koodia katsoessani, ei jotkut kohdat tästä kuitenkaan aukea minulle kuten ei myöskään ehkä muillekaan ja toivoisinkin, että seuraavalla kerralla palattaisiin vielä tähän, vaikka olemmekin siirtyneet jo päätöksentekoanalyysin maailmaan. Tässä kohta, mikä on vielä epäselvä tagged[d]~dbin(1,1000)}. Mistä nämä numerot tulevat?

Olemme blogissa pohtineet paljon mallin kehittämiseen liittyviä kohtia, kuten lisäpyydyksen huomioimista ja vaelluspoikasten muuttointensiteetin mallintamista. Varovainen arvioni on, että kaikesta malliin liittyvästä epävarmuudesta huolimatta, olemme olleet tyytyväisiä sen kehittymiseen. Edelleen mielessämme on ollut useita parannusehdotuksia, kuten veden lämpötilan ja korkeuden sekä vaellusmatkan pituuden huomioiminen. Blogipohdinnat ovat siirtyneet enemmän päätöksentekoon liittyviin kysymyksiin, mutta palaan vielä hetkeksi takaisin mallintamisen maailmaan ja aiheeseen, joka on jäänyt itselleni hyvin epäselväksi, ja jota ei vielä ole nostettu blogissa tarkemmin esille: Milloin malli on oikeasti valmis?

Tutkijana painii jatkuvasti omaan työhön kohdistuvan epävarmuuden kanssa. Työstä pitäisi sanoa jotain konkreettista, mutta samalla joutuu tiedostamaan, että työhön liittyy enemmän tai vähemmän epävarmuutta. Kurssilla olen ensimmäistä kertaa harjoittelemassa todennäköisyysmallintamista, ja oppiminen on kohdistunut perusasioiden haltuun ottamiseen ja BUGS-ohjelman ymmärtämiseen. Bayes-maailma on minulle vielä hyvin uusi, mutta kurssin edetessä olen pohtinut, milloin mallin kehittäjä voi olla tyytyväinen aikaansaannokseensa ja valmis esittelemään sen yleisölle.

Biologina jotenkin kuvittelisi, että malli on valmis silloin, kun se kuvaa luonnossa tapahtuvia prosesseja parhaiten. Miten tämä voidaan varmistaa, onkin sitten toinen tarina. Tuleeko kaikki mahdolliset (ympäristö)tekijät olla mukana mallissa? Tilastotiedettä opiskelevat kurssikamut ovat kuitenkin saaneet minut pohtimaan asiaa toisesta näkökulmasta. Ehkä malli onkin valmis silloin, kun se on rakennettu ”oikein ja ammattitaidolla”. Aiemmissa blogipostauksissa on nostettu esiin myös asiantuntijatieto. Olettaen, että asiantuntijatieto on lähellä ”oikeaa totuutta”, onko valmis malli sellainen, joka vastaa asiantuntijan tietoa tai näkemystä?

Myönnettäköön, että kysymys on tällä erää ehkä lähinnä filosofinen, mutta käsitys kehitysprosessista kokonaisuutena on minulle vielä melko tuntematon. Varsinkin kun olemme jättämässä mallin kehittelyn, jotta voimme käsitellä päätösanalyysiä loppukurssin ajan. Pääsimmekö kunnolla edes vauhtiin vai raapaisimmeko vasta pintaa?

Ajaessani tänään Vanhankaupunginkosken yli, huomasin sivusilmällä smolttirysän olevan jälleen käytössä tauon jälkeen. Rysä oli asennettu nyt pyytämään eri kohtaan jonkin matkaa ylävirtaan edellisestä paikasta ja tällä kertaa enemmän uoman länsipuolelle. Liekö virtaus jälleen käynyt epäsuotuisaksi ruuvipyydyksen käytölle.

Kuten porukalla keskustelimme edellisellä kokoontumiskerralla, olisi pyydysten pyyntitehon määrittämisen kannalta paras vaihtoehto, mikäli pyydykset olisivat mahdollisimman ”tasapaksussa” kohdassa jokea, mistä kalat laskeutuisivat mahdollisimman sattumanvaraisesti ohi. Tällöin voitaisiin arvioida pyydyksen pyyntitehoa suoraan osuutena uoman poikkileikkauksen pinta-alasta, jonka pyydys kattaa. Ruuvin pyytäessä tällä hetkellä hyvin epätasaisessa kohdassa jokea itähaaran puolella, selkeän päävirran kohdalla, ei pystytä näin selkeätä laskelmaa tekemään. Epätasaisessa, leveydellään virtauksien puolesta vaihtelevassa uomassa saattaa laskeutumisreiteissä etenkin eri virtaamilla esiintyä suuriakin vaihteluita. Smolttiruuvin asentamispaikkaan vaikuttaa pyydyksen tekniset edellytykset, sen vaatiessa tietyn virtauksen ja hiljaa virtaavan, tasaisen suvannon virtaus ei riitä pyörittämään ruuvin rumpua. Rysällä puolestaan ei ole vastaavia vaatimuksia virtauksen suhteen. Rysän edellinen pyyntipaikka oli kuitenkin heti saarekkeen yläpuolella, missä ainakin silmämääräisesti näyttää, että virta alkaa vaihdella enemmän, kuin ylempänä suvannossa ja esimerkiksi toista haaraa suosivat kalat ovat saattaneet jo ryhmittyä tietylle puolelle jokea epäsattumanvaraisesti.

Rysän uusi pyyntipaikka hieman ylempänä vastaa paremmin kalojen koko uoman leveydelle satunnaisesti levittäytymisen edellytyksiä. Muuttamalla pyydysten paikkoja tutkimusjakson aikana, tulee kuitenkin pyydysten tehon ja hierarkkisesti edelleen myös vaeltavien smolttien kokonaismäärän arvioimiseen mukaan lisää epävarmuustekijöitä.

Tietysti huolellisellakaan tutkimussuunnittelulla ei pystytä aina vaikuttamaan muuttuviin olosuhteisiin ja suunnitelmia joudutaan muuttamaan. Meidän osalta hommahan etenee lähtökohtaisestikin melko nurinkurisesti. Parempaan lopputulokseen varmastikin päästäisiin, mikäli koko projekti olisi aloitettu mallien alustavalla suunnittelulla ja tutkimusasetelmaa olisi lähdetty kehittelemään mallien ehdoilla.

Helsingin Vanhankaupunginkosken padon purkamisen hyödyistä ja haitoista on väitelty viime vuoden syyskuusta lähtien. Tuuli bloggasi asian tiimoilta viime sunnuntaina (https://blogs.helsinki.fi/taimenlaskenta/?p=163.); Helsingin Sanomat kirjoitti aiheesta viimeksi eilen (http://www.hs.fi/kaupunki/a1305954428529).

Kaupunginhallituksen kokouksessa päätettiin vastikää yksimielisesti palauttaa padon purkuehdotus uudelleen valmisteltavaksi.  Nähtiin tarpeelliseksi lisäselvitysten tekeminen padon purkamispäätöksen mahdollisista vaikutuksista ennen kaikkea alueen kalastoon, vuollejokisimpukoihin sekä Pikkukosken uimarannan vapaa-ajankäyttöön.

Näiden tekijöiden lisäksi kaupunginhallituksen päätöksen (purkaa tai jättää purkamatta pato) vaakakupissa tulee varteenotettavina arvoina painamaan ainakin padon ja voimalan museaalinen ja esteettinen arvo, sekä jossain määrin myös voimalan tuottama sähkö (http://jukkarelander.puheenvuoro.uusisuomi.fi/177564-miksi-vanhankaupunginkosken-pato-kannattaa-purkaa).

Päätös siitä, mitä tulisi tehdä, on määritelmällisesti normatiivinen ja siten luonteeltaan myös eettinen. Jos eettinen tarkastelu rajataan seurausetiikkaan (intuitionistiset, velvollisuus- ja hyve-eettiset pohdinnat sivuuttaen), voidaan rationaalinen eettinen päätös padon purkamisesta palauttaa seurausten haittoihin (tai kääntäen hyötyihin) ehdolla vaihtoehtoiset, mutta toteutettavissa periaatteessa olevat toimintamallit. Yksinkertaisimmillaan käsillä oleva päätöksentekotilanne voitaisiin siis hahmottaa seurausten hyödyillä/haitoilla ehdolla padon purku versus padon säilyttäminen (käytännössä ehdotetut toimintamallit ovat toki hienosyisempää mallia: padon purku JA .. versus padon säilyttäminen JA..).

Mutta: omenia ja appelsiineja; esteettisiä, luonnonsuojelullisia ja vapaa-ajanvietollisia arvoja: miten näitä voidaan vertailla keskenään?

Jos ei voitaisi, kaupunginhallituksen päätös kerätä lisätietoa potentiaalisten toimintamallien mahdollisista seurauksista olisi lähtökohtaisesti älytön. Jos hyödyt nähtäisiin yhteismitattomina – tai yhtä lailla jos tiedettäisiin jokin hyöty painoarvoltaan dominoivaksi kaikissa mahdollisissa maailmoissa – ei keskustelua erilaisista skenaarioista tarvitsisi käydä (jolloin väittäisin sitä ironisen paradoksaalisesti todennäköisesti käytävän loputtomiin). Riittäisi todeta joko: ”minä pidän padoista, sinä kaloista – siinä kaikki!” tai: ”padon museoarvo on suurempi kuin suurin kuviteltavissa oleva kalakantahävikki”. End of discussion.

Lisäinformaatio olisi yhtä lailla hyödytöntä, jos jo tiedetään, mitä toimintaskenaarioille ehdollisista seurauksista voidaan ylipäänsä tietää. Tällainen tilanne on vastassa kahdessa ääripäässä: 1) jos toimintamalleihin liitettäviin mahdollisiin maailmoihin ei liity epävarmuutta lainkaan, tai 2) päätöksenteko on luonteeltaan niin toivottoman epävarmaa, että mahdolliset maailmat voivat olla yhtä hyvin aivan mitkä tahansa. Näiden ääripäiden välissä tulee pohtia lisäinformaatiosta saatavia päätöksenteolle suhteellisia kustannushyötyä.

Juuri koskaan ei tiedetäkään kaikkea (eikä varmuudella juuri muuta kuin analyyttiset totuudet, kuten: “jos pato puretaan, patoa ei enää ole“). Lähes yhtä harvoin päätöksentekotilanne on toivottoman epävarma. Harvojen preferenssit ovat myöskään täysin ehdottomat, vaan jossain tulee myös äärimmäisellä henkilöllä vastaan vaihtosuhde yhden versus toisen preferenssin suosimisen välillä. Näin on aina, kun padon esteettinen hyötyarvo ei ylitä äärettömän kalan hyötyarvoa jne (huono esimerkki siinä mielessä, että hyötyfynktion yli kalojen tulee olla vahvasti laskeva siihen pisteeseen, että äärettömän monen kalan lisä olisi äärettömän epämukavaa).

Siksi lähes kaikissa päätöksentekotilanteissa on kyse 1) vaihtoehtoisten maailmojen sisältämien hyötyjen vertailemisesta keskenään, sekä 2) näiden hyötyjen painottamisesta maailmojen todennäköisyyksillä ehdolla valittu toimintamalli. Tähän päättelytilanteeseen voi bayesilainen päätöksentekotiede tarjota parhaat mahdolliset välineet. Esimerkiksi Vantaanjoen smoltteja estimoidessa voidaan arvioida, kuinka paljon taimenia muuttaa Vantaanjoesta mereen ehdolla pato versus ehdolla ei patoa. Mahdollisten maailmojen todennäköisyyksien määrittämiseen liittyvä mallivalinnan epävarmuus voidaan huomioida keskiarvoistamalla yli käytettyjen todennäköisyysmallien (https://blogs.helsinki.fi/taimenlaskenta/?p=133).

Julkisessa päätöksenteossa maailma monimutkaistuu entisestään: huolella estimoidut mahdollisten maailmojen todennäköisyydet tulisi liittää henkilöittäin vaihteleviin hyötyihin aggregaattitasolla siten, että sosiaalinen hyötyfunktio kuvaa parhaalla mahdollisella tavalla yksittäisiä preferenssejä. Bayesilainen päätöksentekotiede kykenee määrittämään mahdollisten maailmojen posterioritodennäköisyydet ehdolla havaittu aineisto. Jos näihin maailmoihin liitettäviä hyötyjä haluttaisiin painottaa perustellulla tavalla yli demokraattisesti validien preferenssien, tulisi bayesilainen teoria edelleen yhdistää sosiaalisen valinnan teoriaan.

Tilastollista päättelyä voidaan harrastaa kahdesta hieman filosofisesti toisistaan poikkeavasta näkökulmasta. Tämä blogi keskittyy ns. Bayeslaisen koulukunnan tarjoamiin menetelmiin. Toinen päättelyn koulukunta on ’perinteisempi’ ja suositumpi frekventistinen päättely. Teoreettisesti ero näiden kahden välillä muodostuu pienestä yksityiskohdasta: Bayes-päättelyssä kiinnostuksen kohteena oleviin mallin parametreihin kiinnitetään todennäköisyysjakauma, kun taas frekventisessä päättelyssä ne ajatellaan tuntemattomiksi, mutta kiinteiksi.

Tämä yksityiskohta osoittautuu hyvin merkitykselliseksi ja määrittelee oikeastaan kaksi hyvin toisistaan poikkeavaa näkökulmaa tilastolliseen päättelyyn. Frekventistisessä näkökulmassa aineiston tuottaneen tilastollisen mallin parametrit ajatelleen siis kiinteiksi, jolloin kaikki käsiteltävä satunnaisuus liittyy itse aineistoon. Aineisto ajatellaan satunnaiseksi leikkimällä sillä mahdollisuudella, että oltaisiin voitu kerätä/havaita myös toisenlaisia aineistoja, mikäli sama koe oltaisiin toistettu samoissa olosuhteissa.

Bayeslaisessa näkökulmassa tilastollisen mallin parametreille kiinnitetään todennäköisyysjakauma, jota päivitetään havaitun aineiston perusteella. Tämä ns. priorijakauma kvantifioi ilmiöön liittyvän enakkotiedon ja siihen liittyvän epävarmuuden. Asetelma on siis päinvastainen kuin frekventistisessä päättelyssä; aineisto on kiinteä ja sen tuottaneen tilastollisen mallin parametrit satunnaisia (epävarmoja).

Tyypillisesti tilastotieteilijöille opetetaan lähinnä pelkästään frekventististä päättelyä. Sellainen asetelma, jossa kaikki onkin toisinpäin aiheuttaa hieman totuttelemista. Olemme esimerkiksi tässä blogissa raportoineet laskentamallimme tuloksia osittain epäselvästi johtuen omalta osaltani kokemattomuudesta analysoida bayslaisen laskentamallin tuloksia. Puutun nyt muutamaan virheelliseen ilmaisuun ja selvennän, mitä yritettiin sanoa ja mitä olisi pitänyt sanoa.

Kokonaismäärän odotusarvon piste-estimaatti

Laskentamallimme tarkoituksena on tuottaa taimenten kokonaismäärän todennäköisyysjakauma. Kun olemme onnistuneet tämän jakauman tuottamaan, on sen odotusarvo meille tunnettu. Käytämme kuitenkin laskennallisia menetelmiä, joten emme aivan täsmälleen pysty tuottamaan haluamaamme jakaumaa, vaan BUGS-ohjelmiston tuottaman estimaatin siitä. On aivan oikein puhua piste-estimaatista, mutta on syytä ymmärtää, että kysymyksessä on estimaatti laskennallisista syistä. Tämä liittyy alempaan kohtaan.

Odotusarvon piste-estimaatin 95% luottamusväli

Luottamusväli on frekventistisen päättelyn termi. Frekventistisessä päättelyssä 95% luottamusväli tarkoittaa, että muodostettu väli sisältää todellisen parametrin arvon 95 kertaa sadasta, perustuen sellaiseen mielikuvitusleikkiin, jossa kerätään vastaavia aineistoja ja muodostetaan uusia välejä.  Tällä nimikkeellä olemme raportoineet kokonaismäärään liittyviä todennäköisyysvälejä (Näistä käytetään Bayeslaisessa analyysissa joskus termiä uskottavuusväli, engl. credible interval), eli sellaisia välejä, joiden sisällä kokonaismäärä on 95% todennäköisyydellä.

Vaikkakin oletettavasti lukijat ovat tienneet mitä näillä luvuilla on tarkoitettu, on niiden kohdalla tarkalleen ottaen tehty paha virhe liittyen edellisen kohdan huomioihin. Kuten todettu, liittyy odotusarvon piste-estimaattiin laskennallista epävarmuutta, joka on tunnettua, sillä laskentaohjelmistot kuten BUGS raportoivat samplaykseen liittyvän epävarmuuden (MCMC error), joka kunkin tunnusluvun kohdalla kuvaa siihen liittyvää laskennallista epävarmuutta. Tämä epävarmuus voitaisiin (ja kuuluisikin) raportoida, jolloin voitaisiin esimerkiksi kertoa piste-estimaattiin liittyvä 95% todennäköisyysväli (uskottavuusväli). Tämä väli on kuitenkin aivan eri asia, kuin mallin antama todennäköisyysväli kokonaismäärälle, sillä piste-estimaatin todennäköisyysvälissä kysymyksessä on parametriin liittyvä laskennallinen epävarmuus, ei mallin epävarmuus.

Raportoimamme luvut ovat siis olleet kokonaismäärän 95% todennäköisyysvälejä – välejä, joiden sisällä kokonaismäärä on mallimme mukaan 95% todennäköisyydellä.

Jatkan seuraavassa Henrin edellisessä postauksessa tekemää oikeellista havaintoa, jonka mukaan smolttien päivittäisen muuttointensiteetin estimoinnissa ei ole (bayesilaisten periaatteiden vastaisesti) käytetty kaikkea käytössä olevaa asiantuntijatietoa.

Siispä kysymys seuraavassa kuuluu: miten sisällyttää (bayesilaiseen tilastolliseen analyysiin) epävarma, mutta samalla huipukas priori? Oletetaan:

1) että menneen tiedon valossa tiedetään kiinnostuksen kohteena olevan satunnaismuuttujan jakauma varsin huipukkaaksi (yhdellä tai useammalla huipulla) sekä

2) että tämän huipun paikan arvioiminen on varsin epävarmaa.

Toisin sanottuna, että tiedetään ennen aineiston keruuta suuren osan käsiteltävän satunnaismuuttujan todennäköisyysmassasta sijaitsevan jollain varsin kapealla, mutta etukäteen huonohkosti tunnetulla tai jopa täysin tuntemattomalla välillä määrittelyjoukkoa.

Tämän kaltainen haaste tulee vastaan smolttien muuttomäärien estimoinnissa, kun tilastollisen mallin puitteissa pyritään määrittämään muuttointensiteetin (eli yksittäisen smoltin merelle lähtemisen todennäköisyyden) jakaumaa tarkasteluajanjakson (1,2,3,4…,60) päivien funktiona. Tiedetään nimittäin, että smoltit (sekä taimenen että lohen) muuttavat melko intensiivisissä, mutta ajoitukseltaan paljon vaihtelevissa muuttopiikeissä. Merkittävän lisähaasteen vaellusmäärien päivittäiselle estimoinnille asettaa se, että havaintopiikkejä vaikuttaisi useimmiten olevan useampia (eli että muuttointensiteetin jakauma on multimodaalinen). Esimerkiksi Tornionjoessa tehdyissä riista- ja kalatalouden tutkimuslaitoksen lohismolttien muuttomäärien arvioinneissa on havaittu kolmehuippuisia muuttojakaumia. Myös taimenten vuosittaisissa muuttomäärissä on havaittu kevään ja kesän kuluessa useita melko jyrkkiä huippuja. (RKTL, 2003, 2008, 2009, 2011, 2012, 2013: kiitos näiden tutkimusten esille nostamisesta kuuluu Sara Enbergille! J)

(Kiinnostava kysymys on, mistä tämä multimodaalisuus johtuu? Modaalisuushan on sinänsä varsin ymmärrettävää huomioiden kalojen ryhmäkäyttäytyminen sekä altistuminen samoille ja oletettavasti jokseenkin samankaltaisesti kuhunkin smolttiin vaikuttaville ympäristötekijöille. Mielestäni toistuva useamman moodin havainto kertoo ainakin siitä, ettei muuttoon lähteminen ole kovin yksinkertainen prosessi, joka olisi suoraan riippuvaista esimerkiksi sopivan lämpötilan saavuttamisesta. Sen sijaan muuttoajankohtaan vaikuttavia ehtoja (”selittäviä ympäristötekijöitä”) on joko useita (ja) tai kalat muuttavat muuttohuipun ympärille muodostuneissa ryhmissä, kalojen kunkin ryhmän sisällä jakamien ominaisuuksien perusteella (”selitettävä” muuttuja eli todennäköinen lähtöpäivämäärä ositettu kalan ominaisuuksin vaihteleviin ryhmiin).

Karkeana esimerkkinä ensin mainitusta voisi olla tilanne, jossa muuttointensiteetin riittävä ehto on riittävän korkea lämpötila, mutta välttämätön ehto sopiva vedenkorkeus. Tällöin vedenkorkeuden vuosittainen vaihtelu kolmessa piikissä voisi selittää kolmihuippuisen muuttointensiteetin jakauman sen jälkeen, kun lämpötilan riittävä ehto on saavutettu. Vastaavasti, jos muuttopäivämäärä riippuu ympäristötekijöiden sijaan tai lisäksi kalan henkilökohtaisista ominaisuuksista, kuten smoltin koosta, smolttien jakautumisesta kutakuinkin kolmeen ryhmien sisällä enemmän kuin välillä vaihtelevaan kokoryhmään selittäisi kolmihuippuisen muuttojakauman.)

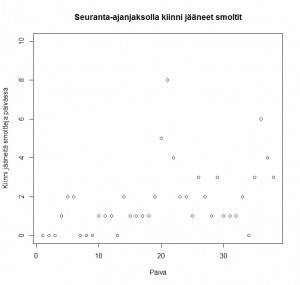
Myös kokonaismuuttomäärien arvioinnin kannalta on varsin tärkeää kyetä estimoimaan, milloin muuttohuippu oikein saavutetaan. Muuttomääriä koskevalla priorivalinnalla on aivan erityisen suuri merkitys juuri silloin, kun havainnointi on vaikeaa, eikä estimointia voida tehdä pelkästään aineistoperusteisesti. Jos (ja meidän tapauksessa kun) yksittäisiä pyydykseen jääviä smoltteja on kovin vähän, on vaihtelu absoluuttisissa pyydykseen jääneiden smolttien havaintomäärissä pientä jopa muuttohuipun ja -suvannon välissä. Kuten mallistamme tiedetään, havaitut muuttomäärät ovat todellisten muuttomäärien ja pyydystettävyyden funktio: jos molemmat näistä selittävistä tekijöistä saavat pieniä arvoja, jää myös pyydykseen keskimäärin vähän kaloja. Tästä seuraavat pienet absoluuttiset havaintomäärien vaihtelut voidaan tällöin virheellisesti arvioida muuttohuipuiksi, varsinkin kun tähän pieneen vaihteluun yhdistetään pyydyksen pyydystettävyyden suuri vaihtelu päivien yli. Vedenkorkeudesta riippuen joinain päivänä ruuvi on pyörinyt, toisina ei. Tietoa siitä, kuinka paljon tämä on vaikuttanut pyydystystehoon, ei ole.  Täten pyydystettävyyden vaihtelua ei ole huomioitu vielä yhtään millään tavalla rakentamassamme pyydystettävyyden tilastollisessa mallissa: tämän seurauksena havaintoperusteiset oletukset muuttopiikeistä voisivat selittyä yhtä lailla todellisella muuttomäärien vaihtelulla kuin käytetyn mittausmenetelmän vaihtelulla (jonkinlaisella systemaattisella mittausvirheellä).

Multimodaalista muuttomäärien jakaumaa ei voida approksimoida millään esittämistämme tilastollisista malleista: tasajakaumamalli olettaa muuttomäärän tasaiseksi (huiputtomaksi) päivien funktiona, lognormaalijakauma olettaa yhden huipun saavutettavan tarkasteluajanjakson alkupäässä, normaali keskellä. Mikään ei kuitenkaan estä sovittamasta mitä tahansa muuttojakaumaa halutulla tavalla kuvaava funktiota, kunhan tämä täyttää todennäköisyysjakauman määritelmän summautuen yhteen yli määrittelyjoukkonsa eli 60 havaintopäivän. Yksi vaihtoehto olisi useamman asteen polynomifunktio. Jonkinlainen kenties helpommin hahmotettavissa oleva approksimaatio käytössä olevan prioritiedon mallintamiseksi saattaisi olla osittaa määrittelyjoukko oletettuihin ”moottohuippuryhmiin” (kuten kolmeen osaan), sovittaa kuhunkin näistä väleistä välin päätepisteisiin katkaistu ja melko huipukas normaalijakauma ja normalisoida saadut tulokset sellaisella vakiolla, joka varmistaa y-arvojen summautumisen yhteen koko 60 päivää kattavassa määrittelyjoukossa.

Miten määrittelyjoukkon ositteiden keskipisteet eli muuttohuiput sitten määritettäisiin? Muuttohuippujen paikkaan (eli seurantajakson ajankohtaan) liittyvää epävarmuutta voitaisiin ainakin vähentää estimoimalla huippukohtaa malliperusteisesti. Bohlin ym. (1993: kiitos tämän tutkimuksen esille nostamisesta kuuluu Mikko Hynniselle) havaitsivat, että muuttopiikin sijoittumiseen vaikuttaa 1) (vuosittaisen) smoltin (keskimääräinen) pituus, 2) vedenkorkeus sekä erityisesti vedenkorkeuden muutos, 3) lämpötila sekä erityisesti lämpötilan muutos (viikon takaisesta) ja 4) edellisen vuoden kalakannan kasvu. Näillä tekijöillä Bohlin ym. kykenivät selittämään 47% prosenttia päivittäisten muuttotodennäköisyyksien varianssista.

Periaatteessa meillä olisi käytettävissä kerättyä seurantatietoa 3 ensin mainitusta tekijästä; neljännestäkin tietoa luulisi olevan saatavilla. Muuttointensiteetin jakauman estimointi mainituilla selittävillä muuttujilla on siis harkitsemisen arvoinen asia. Tällaisellakin (polynomiaalisella regressio)mallilla jäisi kuitenkin edelleen oletettavasti selittämättä suurin osa smolttien muuttoon lähtötodennäköisyyden päivittäisestä vaihtelusta, minkä lisäksi ei voitaisi tietenkään mennä takuuseen siitä, että lounais-Ruotsissa tehdyt havainnot siirtyvät sellaisenaan Vantaanjoen kaikin puolin varsin erityislaatuiseen muuttotilanteeseen. Siksi tällaiseenkin regressiomallivalintaan tulisi suhtautua terveellä skeptisyydellä kuitenkin samanaikaisesti ymmärtäen, että kaikki käytössä oleva tieto olisi syytä estimoinnissa myös hyödyntää: lähes täydelliseen a priori tietämättömyyteen perustuva malli on peräti virheellinen (ja tehoton), jos a priori tieto on oikeasti olemattoman sijaan ainoastaan heikkoa.

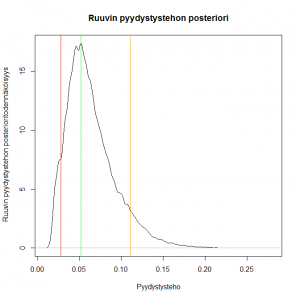
Muuttomäärien jakaumaa koskeva arvio on vaikutusvaltainen kokonaismääriä estimoitaessa. Tämän voi havaita tarkastelemalla eri mallivalintojen posterioriestimaatteja Vantaanjoen smolttien muuttomääristä (ks. tämän päivän tulospostaus kolmella mallilla). Tästä seuraa yhdessä mallivalintaan liittyvän edellä esitellyn epävarmuuden kanssa, että vuosittaisen muuttomäärän totaalin posterioriestimaattia johtaessa olisi järkevää käyttää melko useaa mallia, joiden yli posterioriestimaatit sitten keskiarvoistettaisiin painottamalla lähtökohtaisesti perustelluimpina pidettyjä malleja suuremmilla prioritodennäköisyyksillä.

Tästä voitaneen luvata tulevan pian lisäpäivityksiä, so stay tuned.