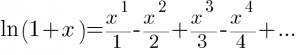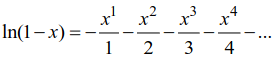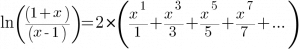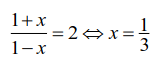Hello, algorithm enthusiasts! If you want to find the easiest route to glory, Simulated Annealing (SA) is just for you. If you’re up against a big and complex problem, this mind-blowing algorithm finds the easiest way to solve it. Just like magic! Visualise SA as a huge bouncing ball on a quest to find the most efficient solution, navigating a landscape of peaks and valleys to reach the treasure at the lowest point.
Our 40-year-old trusty sidekick SA, was born in 1983 to tackle nonlinear problems, inspired by the annealing process in metallurgy. At the start of every journey to find the lowest point, SA, the huge bouncing ball, jumps through different altitudes and obstacles. Everything is high at the beginning for our daring adventurer; the altitude, the energy, and the expectations. With the high energy, it can leap over immense mountains, with every jump creating temperature. As the altitude drops, the temperature drops as well, and instead of those intense jumps, our adventurer becomes more selective as a clearer path emerges in the valleys…
The annealing schedule to control the temperature determines how much uphill movement SA allows. Choosing the right schedule is crucial. Start with a high initial temperature, “melting” the system, and gradually reduce it as the search progresses. Finding this balance ensures SA explores extensively at the start but narrows down to the optimal solution.
The algorithm involves four key components: a representation of possible solutions, a generator of random changes, an evaluator for problem functions, and an annealing schedule which is a road map for temperature reduction during the search.
SA shows its brilliance in chaotic data because of its random search capability. One of the biggest issues that the more traditional friends of SA face is getting stuck in a local minimum, which means falling into a hole other than the lowest point, and failing to get out of it. However, our daring adventurer randomly accepts challenges and doesn’t shy away from climbing uphill. In other words, since SA doesn’t rely on strict model properties, it has the power of bypassing the local minima.
Even with these impressive features, in the optimisation arena, SA has some ambitious competitors like Neural Nets and Genetic Algorithms. Unlike Neural Nets that learn by strictly following one function, SA is a smart random searcher, which is an advantage as known in the local minima. When pitted against Genetic Algorithms, SA often emerges victorious, offering a global convergence guarantee.
SA is a probabilistic optimisation algorithm, that allows its versatility in problem solving. On the other hand, this means that a lot of time and precision in inputs is required for the quality of the solution. Implementing SA requires defining solutions, generating random changes, evaluating functions, and setting up the annealing schedule. Another vital part in these phases is the implementation of covariance matrices which show the distribution magnitude and direction of multivariate data in a multidimensional space. (Multivariate data refers to datasets that involve more than one variable.)
Now, you might wonder, “Why does SA matter to me?” Well, if you’re dealing with financial instruments, SA is becoming the go-to algorithm for hybrid securities and intricate trading strategies as its flexibility stands out while also having the ability to navigate complexities of multivariate systems, blending continuous and discrete sets seamlessly.
In a nutshell, SA is a flexible and robust optimisation tool that excels in navigating complex landscapes. While it may be computation-intensive, its prowess in tackling nonlinear problems makes it a hero in the world of optimisation.
So, optimisation enthusiasts, whether you’re crunching numbers in finance or exploring intricate models, consider adding Simulated Annealing to your toolkit. It might be just the adventure you need to overcome your optimisation challenges by diving to the lowest point.
Stay optimised, stay curious!
Prepared By: Ali Onur Özkan
Article Reference: Busetti, F. (2018, December 10). (PDF) simulated annealing overview – researchgate. ResearchGate. https://www.researchgate.net/publication/238690391_Simulated_annealing_overview