Petro Poutanen's blog – Miscellaneous notes from my researcher years

Hajontakuva luokitellun muuttujan visualisoinnissa

Hajontakuva (scatterplot) on yksinkertainen ja helppo tapa kuvata kahden jatkuvan muuttujan välistä yhteyttä. Tavallisesti y- eli pystyakselille on tapana piirtää selitettävä (dependent variable) muuttuja ja x-akselille selittäjä (independent variable). Muuttujien arvojen leikkauspisteissä ovat havaintoyksiköt (observational units) eli esimerkiksi kyselytutkimuksessa vastaajat. Hajontakuvaa voidaan kuitenkin käyttää myös luokitellun muuttujan visualisoitiin. Tällöin havaintoyksikköinä ovat luokitellun muuttujan arvot ja y- ja x-muuttujina sellaiset luokkien eroja ja yhtäläisyyksiä kuvaavat muuttujat, jotka ovat tutkimuksen kiinnostuksen kohteina. Esittelen seuraavaksi askel askeleelta, kuinka kyseinen toimenpide voidaan toteuttaa SPSS Statistics -ohjelmistolla. Datana käytän Yleisradion verkkopalveluiden kyselyä, joka on Ylen tutkimusdataa ja julkaistu avoimena datana Ylen Kehitys kehittyy –blogissa.

Aineisto

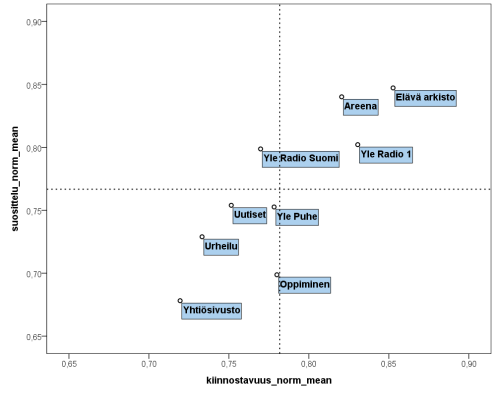
Data sisältää 27.4.–28.5.2013 web-lomakkeella kerättyä palautetta verkkosivujen käyttökokemuksista. Datasta löytyy yhteensä 9000 vastaajaa ja muuttujia on mukana 8 kappaletta. Valitaan kiinnostuksenkohteiksi kolme muuttujaa: sivusto, jolla kävijä on vieraillut (Sivusto), kiinnostavuus asteikolla 0–6 (Kiinnostavuus) sekä suosittelu (halu suositella sivustoa muille) asteikolla 0–10 (Suosittelu). Muuttujien arvot määräytyvät siten, että pienet arvot tarkoittavat vähemmän tai ei ollenkaan muuttujan mittaamaa ominaisuutta. Luokiteltu muuttuja Sivusto saa arvoja sen mukaan, millä sivustolla kävijä on vieraillut eli mihin sivustoon hänen arvionsa kohdistuvat (esim. Elävä arkisto, Uutiset…). Tavoitteena olisi siis kuvata eri sivut hajontakuvassa siten, että y- ja x-akseleilla kulkevat käyttäjien arvioimat kiinnostavuus ja halu suositella sivustoa ja näiden arvojen leikkauspisteissä ovat sivustot. Näin voisimme verrata, mitkä sivut koetaan kiinnostaviksi ja mitä halutaan suositella suhteessa toisiin sivuihin.

Muuttujien standardointi

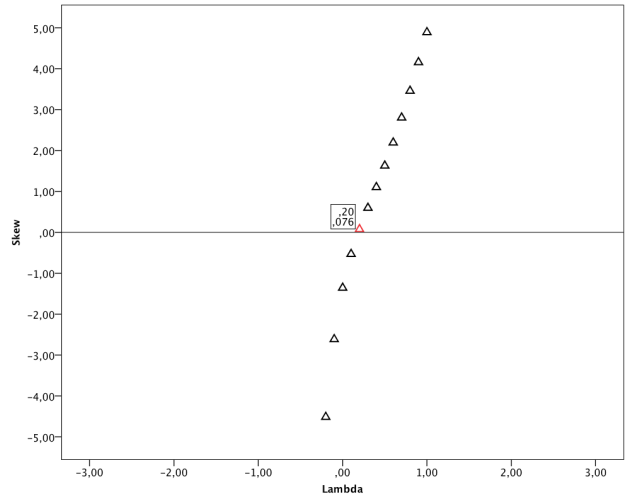
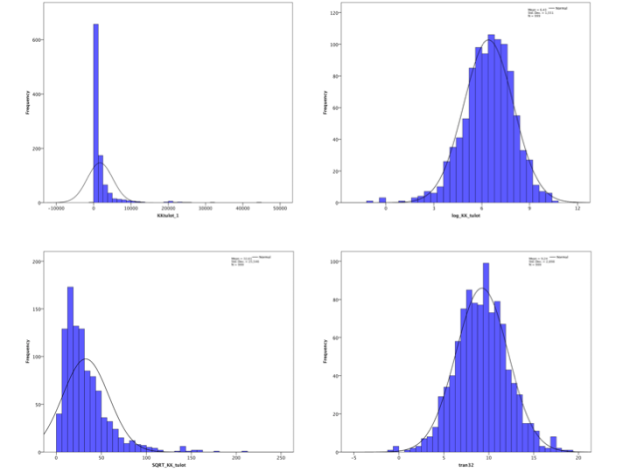
Ennen kuin ryhdymme muuttamaan dataa sellaiseen muotoon, että sen visualisointi hajontakuvana on mahdollista, muuttujien asteikkoja on syytä tarkastella hieman lähemmin. Koska muuttujien vaihteluväli on erilainen (0–6 ja 0–10), ne voidaan standardisoida eli saattaa vertailukelpoisiksi. Tämä voitaisiin suorittaa normeeraamalla eli laskemalla kummastakin muuttujasta Z-pisteet, jossa jakauma “pakotetaan” sellaiseen muotoon, että keskiarvo on 0 ja keskihajonta 1. Normaalijakauman mukaisesti normeeratut arvot vaihtelevat käytännössä välillä -3 ja 3. Vanhat lukuarvot menetetään, mutta uudet ovat keskenään vertailukelpoisia. Lisäksi saadaan tietoa siitä, kuinka monen keskihajonnan päähän keskiarvosta arvot sijoittuvat. Voimme esimerkiksi arvioida, kumpi mitattu ominaisuus on keskiarvoltaan toista suurempi (kiinnostavuus vai halu jakaa). Tämä toiminto tapahtuu SPSS-ohjelmistossa esimerkiksi valitsemalla Descriptives-valikosta “Save standardized values as variables”. Tässä tapauksessa lukuarvoilla ei kuitenkaan ole mitään merkitystä, sillä olemme kiinnostuneita vain visualisoimaan sivustojen suhteellisia eroja hajontakuvan avulla. Normeerauksen sijaan voimme yksinkertaisesti pakottaa muuttujien arvot välille 0 ja 1. Tämä tapahtuu kaavalla

$\ X_{0-1}=\frac{X_{i}-X_{min}}{X_{max}-X_{min}}$

missä “X0-1” on uusi, standardoitu muuttuja, “Xi” on vanha standardoimaton muuttuja ja “Xmin” ja “Xmax” ovat vanhan muuttujan minimi- ja maksimiarvot. Koska muuttujan Kiinnostavuus arvo 0 tarkoittaa “En tunne palvelua”, voidaan kyseinen arvo merkitä puuttuvaksi. Lasketaan uudet muuttujat seuraavalla syntax-kommennolla:

descriptives Suosittelisitko Kiinnostavuus.
compute suosittelu_norm = (Suosittelisitko - 0) / (10 - 0).
compute kiinnostavuus_norm = (Kiinnostavuus - 1) / (6 -1).

Datan aggregointi

Koska tavoitteena on kuvata luokiteltu Sivusto-muuttuja kahden jatkuvan (tai sellaiseksi tulkittavan) muuttujan avulla, täytyy data aggregoida Sivusto-muuttujan luokkien tasolle. Käytännössä tämä tarkoittaa sitä, että luomme uuden datan, jossa Sivusto-muuttujan eri luokkien tasolle lasketaan keskiarvot (tai jotkut muut tiivistävät tunnusluvut). Vaikka muuttujien jakaumat eivät ole täysin normaaleja, voimme tässä tyytyä keskiarvoihin. Aggregointi tapahtuu valitsemalla Data/Aggregate ja sijoittamalla halutut muuttujat kenttiin (Sivusto on “Break variable”) tai seuraavalla kommennolla:

DATASET DECLARE agre.
AGGREGATE
/OUTFILE='agre'
/BREAK=Sivusto
/suosittelu_norm_mean=MEAN(suosittelu_norm)
/kiinnostavuus_norm_mean=MEAN(kiinnostavuus_norm).

Uuden aineiston tulisi näyttää siltä, että ensimmäisellä sarakkeella ovat sivustojen nimet ja seuraavilla muuttujien keskiarvot ensimmäisen muuttujan eri luokissa/arvoilla. Nyt olemme valmiita hajontakuvan piirtämiseen.

Hajontakuvan piirtäminen

Hajontakuvaksi kannattaa valita “Simple scatter”. Perinteisiä konventioita noudattaen pystyakselille valitaan se muuttujan, jota selitetään, ja vaaka-akselille selittäjä eli se, josta pystyakselin muuttuja ikään kuin voisi seurata: X -> Y. On luontevaa ajatella, että sivuston kiinnostavuus (X) selittää (ainakin osin) halua suositella sivustoa (Y) sosiaaliselle verkostolleen, eikä toisin päin. Piirretään kuva siis näin päin. SPSS:n Chart editorilla voidaan lisäksi asettaa luokitellun muuttujan arvojen nimet (label) mukaan kuvaajaan, piirtää kummankin jatkuvan muuttujan keskiarvojen kohdalle referenssiviivat sekä skaalata vaaka- ja pystyakselit samanpituisiksi. Erityisesti viimeinen toimenpide on tärkeä, sillä muuten kuva saattaa vääristää muuttujien välistä suhdetta. Keskiarvosuorien piirtämä nelikenttä auttaa hahmottamaan, mitkä havainnoista osuvat kunkin muuttujan keskiarvon ylä- ja alapuolelle. Kun yhteys on positiivinen, oletettavaa on että ne sivustot, jotka ovat keskiarvon yläpuolella kiinnostavuudessa, ovat sitä myös suosittelussa. Näin näyttäisi pääpiirteissään olevan. Lisäksi voidaan todeta, että yhteys kiinnostavuuden ja suositteluhalun välillä on lineaarista: mitä kiinnostavampi sivusto, sitä todennäköisemmin sitä voitaisiin suositella myös muille.

Hajontakuva Ylen verkkosivustoista kiinnostavuuden ja suositteluhalun suhteen.

Postaus on julkaistu alun perin 29.5.2013.

Hajontakuvan “tärisyttäminen” SPSS:llä (jittering with SPSS)

Hajontakuvan (scatterplot) avulla kuvataan tavallisesti kahden muuttujan yhteisvaihtelua pisteinä kaksiulotteisella tasolla. Hajontakuvaa voi käyttää niin jatkuvien kuin kategoristenkin muuttujien visualisoinnissa. Erityisesti kyselyaineistoissa muuttujat ovat harvoin jatkuvia “ikää”, “tuloja”, tms. lukuun ottamatta. Likert-asteikolla kysyttyjen kysymysten välimatka-asteikollisuus tulee tylsällä tavalla esiin kuvattaessa muuttujien yhteisvaihtelua hajontakuvan avulla: kuvassa näyttäisi olevan vain muutama datapiste, vaikka todellisuudessa niitä voi olla useita satoja päällekkäin. Tällöin kuvan toiset pisteet voivat näyttää toisia tummemmilta, mutta yleiskuvaa yhteisvaihtelusta ei tällaisen visualisoinnin avulla saa (ks. alla olevassa kuvassa vasemmanpuoleista hajontakuvaa). Onneksi tähän yleiseen ongelmaan on olemassa kätevä ratkaisu, nimittäin kuvan datapisteiden tärisyttäminen (jittering).

Tärisyttäminen tarkoittaa sitä, että datapisteen sijaintiin lisätään hieman satunnaista kohinaa kummankin akselin suuntaisesti. Koska kohina kohdistuu kaikkiin datapisteisiin tasaisen satunnaisesti, efekti ei muuta itse vaihtelua, vaan tuo sitä paremmin näkyville; toistensa päälle sijoittuneet datapisteet pääsevät näkyviin (ks. kuvan kaksi oikeanpuoleista hajontakuvaa).

Yllä olevassa kuvassa on kolme eri hajontakuvaa, joissa pystyakselilla kulkee koettu terveydentila 5-portaisella asteikolla ja vaaka-akselilla ikä (aineisto: ESS-Suomi, 2010). Ensimmäinen on selvästi välimatka-asteikollinen ja jälkimmäinen jatkuva muuttuja. Ensimmäisestä kuvasta on vaikeaa saada käsitystä muuttujien yhteisvaihtelusta, sillä kaikki datapisteet kasaantuvat riveiksi iän mukaan tereveydentila-muuttujan viidelle eri arvolle. Jälkimmäiset kaksi kuvaa ovat tärisytettyjä, jälkimmäinen voimakkaammin kuin ensimmäinen. Jälkimmäisistä kuvista näkyy selvästi, että ikä vaihtelee melko hajallaan kahden ylimmän terveydentila-arvon sisällä, kun suurin osa arvoista sijoittuu kategoriaan 4 ja trendi on hieman negatiivinen (koettu terveydentila alenee iän myötä). Saman toimenpiteen voi tehdä myös kahdelle kategoriselle muuttujalle, mikä auttaa hahmottamaan muuttujien vaihtelua toistensa eri luokissa. Tässä alla esimerkki sukupuolesta ja koetusta terveydentilasta.

Viimeisessä esimerkissä (alla oleva kuva) on visualisoitu kaksi jatkuvaa muuttujaa, median käyttö -summamuuttuja ja vastaajan ikä. Tässäkin tapauksessa tärisyttäminen parantaa kuvien luettavuutta. Median käyttö -muuttuja ei ole aidosti jatkuva, vaan eri medioihin kulutetun ajan keskiarvosummamuuttuja, mistä johtuu muuttujan arvojen kerrostuminen ensimmäisessä hajontakuvassa.

Tärisyttäminen SPSS:llä (commands for jittering with SPSS)

SPSS tarjoaa tärisyttämisen suorittamiseksi kaksi toimintoa, joihin pääsee käsiksi vain syntax-komentoikkunan kautta. Ensimmäinen on ohjelman vanhempiin versioihin suunniteltu IGRAPH-toiminto (esimerkeissä keskimmäiset hajontakuvat), joka voidaan suorittaa seuraavalla komennolla (lisää omien muuttujien nimet kohtiin “Y-” ja “X-variables”):

igraph
/Y= VAR(X-variable) TYPE = scale
/X1=VAR(Y-variable) TYPE=SCALE
/COORDINATE=VERTICAL
/SCATTER COINCIDENT=JITTER.

Suorittaessa tämän komennon SPSS (ver. 18) muistuttaa, että IGRAPH-toimintoa ei enää tueta, ja suosittelee siirtymistä GGRAPH-toimintoon. GGRAPH-toiminnosta löytyy tuki kategorisen hajontakuvan tärisyttämiselle, ja se voidaan piirtää seuraavan komennon avulla:

GGRAPH
/GRAPHDATASET NAME="DataSet1" VARIABLES= X-variable Y-variable
/GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
SOURCE: s = userSource(id("DataSet1"))
DATA: Ikä=col(source(s), name("X-variable"), unit.category())
DATA: Y-variable=col(source(s), name("Y-variable"), unit.category())
GUIDE: axis(dim(2), label("Y-variable"))
GUIDE: axis(dim(1), label("X-variable"))
ELEMENT: point.jitter(position(X-variable*Y-variable))
END GPL.

Harmillisesti en ainakaan itse ole löytänyt GGRAPH:sta toimintoa, joka tukisi myös muiden kuin “kategoristen hajontakuvien” tärisyttämistä. Tämä aiheuttaa sen, että kuvien käsittely Output-ikkunassa on ennalta rajattu kategorisia muuttujia varten, ja esimerkiksi regressiosuoran lisääminen kuvaan pitää tehdä syntax-koodin kautta:

ELEMENT: line(position(smooth.linear(X-variable*Y-variable)))

GGRAPH tarjoaa sentään jonkinlaisen tavan määritellä, miten datapisteiden uuden sijainnin arvonta tapahtuu. Muokkaamalla riviä ELEMENT: point.jitter(position(X-variable*Y-variable)), voidaan määrittää mitä jakaumaa arvonta noudattaa – vakiovaihtoehdon olleessa tasajakauma. Lisätietoa löytyy SPSS:n helpistä hakusanalla “jittering”. Julkaistaessa tärisytettyjä kuvia niiden oheen on tapana liittää näkyville tieto tärisyttämisestä.

Postaus on julkaistu alun perin 4.7.2013.

Syntymäpäivätemppu

Eilisen syntymäpäiväni kunniaksi päätin tehdä syntymäpäiväaiheisen postauksen. Moni on ollut ehkä kuuntelemassa (tai katsonut videolta) puhujaa tai luennoitsijaa, joka kysyy, sattuuko kenelläkään yleisössä olemaan syntymäpäivä. Yleensä käsiä aina nousee pystyyn. Voi tuntua sattumalta, että jollakin on syntymäpäivä juuri sinä päivänä, kun sitä kysytään. Onkin kiinnostavaa, mikä on syntymäpäivän todennäköisyys eri kokoisissa yleisöissä. Tähän saadaan teoreettinen vastaus todennäköisyyslaskennan avulla.

Oletetaan, että kaikki syntymäpäivät ovat yhtä todennäköisiä (vaikka ne eivät ole), että niitä on yhteensä 365 kpl ja että syntymäpäivä ei vaikuta yleisön valikoitumiseen millään tavalla (vaihtele siis satunnaisesti suhteessa yleisöön). Tarkastellaan tilannetta, jossa vähintään yhdellä yleisön joukossa on syntymäpäivä. Syntymäpäivän todennäköisyys on 1/365 jokaiselle yleisön jäsenelle, ja todennäköisyys puolestaan sille, että henkilöllä ei ole syntymäpäivää on 364/365. Yleisöjoukon kaikkien mahdollisten alkeistapausten (mahdollisten syntymäpäiväyhdistelmien) määrä on 365 x 365 x 365 … n. Määritellään todennäköisyys “vähintään yhdellä on syntymäpäivä” vastatapahtuman “kenelläkään ei ole syntymäpäivä” avulla: P(vähintään yhdellä on syntymäpäivä) = 1 – P(kenelläkään ei ole syntymäpäivä). Koska yleisön koko on toistaiseksi rajoittamaton merkitään sitä n:llä. Siten:

$\text{P(vahintaan yksi syntymapaiva)} = 1-\left ( \frac{364}{365} \right )^{n}$

Nyt voidaan laskea esimerkiksi että jos n = 1000, niin P = 0.936, eli tuhatpäisessä joukossa vähintään yhdellä henkilöllä on syntymäpäivä jo 94% todennäköisyydellä. Otetaan SPSS avuksi ja tarkastellaan, miten yleisön koko vaikuttaa todennäköisyyteen onnistua löytämään syntymäpäiväsankareita. Luodaan aluksi 1000 havaintoa ja lasketaan sitten kullekin “yleisömäärälle” oma todennäköisyytensä. Piirretään tämän jälkeen nämä vastakkain.

set seed = 100.
 input program.
 loop #i = 1 to 1000.
 compute ID = #i.
 end case.
 end loop.
 end file.
 end input program.
 dataset name birthday.
 execute.
compute P_birthday = (1-(364/365)**ID).
 VARIABLE LABELS P_birthday 'P("vähintään yksi syntymäpäivä")'.
 execute.
GRAPH
 /SCATTERPLOT(BIVAR)=ID WITH P_birthday.

Kuvaajasta huomataan, että todennäköisyydet kasvavat yleisömäärän mukaan logaritmisesti. Kasvu on aluksi nopeaa ja sitten hidastuu kohti ääretöntä. Apuviivojen leikkauspisteestä voidaan poimia “kriittinen raja” sille, kannattaako temppua yrittää eli ovatko mahdollisuudet enemmän kuin fifty-fifty. Tuo raja on 253 yleisön jäsentä, eli tuota kokoa suuremmissa yleisöissä on todennäköisempää että vähintään yhdellä on syntymäpäivä kuin että kenelläkään ei olisi, ja kun n > 500 alkaa todennäköisyys olla jo melko korkealla (>75%). Sama raja voitaisiin tietysti laskea myös yllä esitetystä kaavasta ratkaisemalla n, kun kaavan arvoksi asetetaan 0.5:

$\ 1-(364/365)^{n}=1/2$

$\ \ln(1)-\ln(364/365)^{n}=\ln(1/2)$

$\ 0-n\ln(364/365)=\ln(1/2)$

$\ n=-\frac{\ln(1/2)}{\ln(364/365)}$

$\ n=252.6519888441584876$

PS. Todennäköisyyslaskennassa on esitetty pitkään hieman toisenlaista ja paljon yllättävämpää “syntymäpäiväongelmaa”, jossa etsitään sellaisen joukon kokoa, jossa todennäköisyys sille, että vähintään kahdella henkilöllä on sama syntymäpäivä olisi yli 0.5. Hämmästyttävästi tämä ehto täyttyy jo 23 ihmisen kokoisessa joukossa! Katso miten.

Postaus on julkaistu alun perin 6.11.2013.

Box-Cox-muunnosten tekeminen vinoille jakaumille SPSS:llä

Keskiarvoihin perustuvat tilastolliset analyysimenetelmät edellyttävät miltei aina normaalijakautuneita ja variansseiltaan samansuuruisia muuttujia. Esimerkiksi regressioanalyysin tai varianssianalyysin vastemuuttujalta edellytetään symmetrisyyttä. Sosiaalitieteellisissä aineistoissa muuttujat ovat harvoin täysin symmetrisiä, esimerkkinä vaikkapa tulotaso, joka on oikealle vino ja huipukas. Vinossa muuttujassa suuri osa havainnoista pakkauttuu keskiarvon jommallekummalle puolelle, eikä keskiarvoa voi näin ollen käyttää luotettavasti muuttujan jakauman kuvaamiseen. Monet tilastolliset testit kuitenkin perustuvat jakauman symmetrisyyteen, ja symmetrisyysedellytyksen rikkominen voi johtaa tulosten validiteetin ja yleistettävyyden kärsimiseen sekä testin voimakkuuden ja luottamusvälien epätarkkuuksiin[1].

Vinot muuttujat on melko helppo korjata muunnosten avulla. Tavallisimpia muunnoksia ovat vinon muuttujan logaritmointi, neliöjuuren ottaminen ja käänteisluku. Näillä operaatiolla vinosta muuttujasta voidaan usein tehdä symmetrisempi. Lisäksi on tavallista että muuttujan pienin arvo ankkuroidaan arvoon 1. Tämä muunnos tehdään kahdesta syystä. Ensinnäkin jos muuttuja saa negatiivisia arvoja, logaritmointi tai neliöjuuren ottaminen ei onnistu. Toiseksi ankkurointi juuri arvoon 1 on tärkeää siksi, että esimerkiksi neliöjuuri luvusta välillä 0 ja 1 on suurempi kuin alkuperäinen luku, kun taas neliöjuuri yhtä suuremmista luvuista on alkuperäistä lukua pienempi. Tämä tuntuu hieman epäloogiselta. Negatiivisesti (vasemmalle) vinojen muuttujien jakauma pitää puolestaan aluksi kääntää. Tämä tapahtuu vähentämällä muuttujan arvot sen maksimiarvosta. Tämän jälkeen muuttuja tulisi ankkuroida minimiarvoltaan 1:een.

Kaikkia muunnoksia voi ajatella jonkin vakion y ja tämän pontessin x avulla. Esimerkiksi potenssin arvot lähellä nollaa vastaavat logaritmimuunnosta, 1/2-eksponentti on sama kuin neliöjuuri, 1 tarkoittaa että muunnosta ei tarvita ja kaksi vastaa eksponenttimuunnosta. Käänteislukumuunnoksia voidaan ilmaista negatiivisena potenssina. Siten suuri osa perusmuunnoksista onkin oikeastaan potenssimuunnoksia. Mutta miksi rajoittua vain tiettyihin potensseihin, jos jokin luku esimerkiksi logaritmin ja neliöjuuren väliltä antaisi paremman lopputuloksen symmetrisyyden kannalta? Boxin ja Coxin (1964) esittelemä tekniikka tarojaa menetelmän ideaalin muunnospotenssin löytämiseksi:

$\ y_i^{\lambda}=\frac{(y_i^{\lambda}-1)}{\lambda}\text{ jossa, }\lambda \neq 0$

$\ y_i^{\lambda}= \text{log}_{e}(y_i)\text{ jossa, }\lambda =0$

Kaavan avulla etsitään y:lle siis sellainen potenssin arvo, joka korjaa parhaalla mahdollisella tavalla muuttujan vinoutta. Lambdan optimaalisin arvo vastaa sitä muunnosta, joka muuttujalle kannattaa tehdä edellisessä kappaleessa esitettyjen vastaavuuksien mukaisesti. Tilasto-ohjelmistoissa lambdan määrittäminen tapahtuu tavallisesti etsimällä sellainen lambdan arvo, joka maksimoi suurimman uskottavuuden funktion logaritmin. SPPS:ssä tällaista toimintoa ei kuitenkaan ole valmiina olemassa. Riittävän hyvään lopputulokseen voidaan päästä myös empiirisellä menetelmällä (ks. [1]), eli laskemalla riittävän monella eri lambdan arvolla suoraan datasta erilaisia muunnoksia muuttujalle ja vertaamalla näitä saavutettuun vinouden vähenemiseen. Katsotaan seuraavaksi Box-Cox-muunnosta esimerkin kautta.

Simuloidaan epäsymmetristä dataa SPSS:n Pareto-funktion avulla parametreilla 1238.33 ja 1.6. Tarkoituksena on tuottaa muuttuja, joka vastaisi jossain määrin oikealle vinoa tulojakaumaa minimipalkasta ylöspäin.

NEW FILE.
INPUT PROGRAM.
LOOP #I=1 TO 1000.
COMPUTE KKtulot = RV.PARETO(1238.33, 1.6).
END CASE.
END LOOP.
END FILE.
END INPUT PROGRAM.
EXECUTE.

Saatu muuttuja ei vastaa täysin todellista tulojakaumaa, mutta on siinä määrin oikealle vino (skweness = 5.656) ja huipukas (kurtosis = 45.057), että esimerkiksi keskiarvon laskeminen ei olisi mielekästä. Nyt tällä KKtulot-muuttujalle voidaan hakea ideaalia muunnospontenssia seuraavan syntaksin avulla [1] [2]. Huomaa, että kohtaan “KKtulot” laitetaan sen muuttujan nimi, jolle muunnosta etsitään ja kohtaan “-1240.17” se luku, joka muuttujasta pitää vähentää/lisätä, jotta minimiarvo ankkuroituu 1:een.

COMPUTE var1=KKtulot-1240.17.
execute.
VECTOR lam(61) /tran(61).
LOOP idX=1 TO 61.
- COMPUTE lam(idx)=-3.1 + idx * .1.
- DO IF lam(idx)=0.
-       COMPUTE tran(idx)=LN(var1).
- ELSE.
-   COMPUTE tran(idx)=(var1**lam(idx) - 1)/lam(idx).
- END IF.
END LOOP.
execute.
FREQUENCIES VARIABLES=var1 tran1 to tran61
    /format=notable
    /STATISTICS= SKEWNESS KURTOSIS
    /ORDER=ANALYSIS.
FREQUENCIES VARIABLES= lam1 to lam61
    /format=notable
    /STATISTICS= MINIMUM
    /ORDER=ANALYSIS.

Komento tulostaa 60 erilaista muunnosta muuttujalle KK_tulot vastaavien lambdan arvojen kulkiessa -3:sta +3:een. Alla olevassa kuvassa on piirrettynä hajontakuvaan vinouskertoimen ja lambdan arvoja. Kuvasta voi huomata, että lambdan arvolla 0.20 (eli lähes nolla = logaritmimuunnos) saadaan ideaalitulos, jossa vinous on 0.076.

Seuraavassa taulukossa ovat alkuperäisen muuttujan, tavallisen logaritmi- ja neliöjuurimuunnoksen sekä lambdan arvolla 0.20 lasketut vinous- ja huipukkuus-luvut. On helppo huomata, että Box-Cox-muunnoksen avulla todella löydettiin tehokas muunnospotenssi.

Statistics	KKtulot_1	log_KK_tulot	SQRT_KK_tulot	tran32
Skewness	5,656	-,532	2,193	,076
Kurtosis	45,057	1,245	7,331	,374

Samat muuttujat on esitetty myös histogrammeina alla (alkuperäinen vasen yläkulma, logaritmi oikea yläkulma, neliöjuuri vasen alakulma ja Box-Cox-muunnos oikea alakulma). Vaikka Box-Cox-muunnos löysi vielä logaritmia tehokkaamman potenssimuunnoksen, on kyseenalaista, kuinka paljon eroa näillä kahdella muunnoksella olisi käytännössä. Menetelmä on kuitenkin tehokas tapa löytää optimaalinen muunnos silloin, kun muuttujia ei ole helppo saada riittävän normaaleiksi tavallisin muunnoksin.

[1] Osborne, J. W. (2013). Best Practices in Data Cleaning: A Complete Guide to Everything You Need to Do Before and After Collecting Your Data. Los Angeles: SAGE Publications. (Vastaava PDF-artikkeli täällä.)

[2] Raynald’s SPSS Tools.

Postaus on julkaistu alun perin 25.2.2014.

Quantitative Methods for Communication Students

This document consists of introductory material on quantitative methods. It is aimed at students of communication but is suitable for the other social scientific fields as well. The emphasis will, though, be on observational studies, with a focus on surveys and content analysis. Experimental research settings are not discussed in this document, although they form an essential part of the scientific study of communication. This limitation is due to framing issues, since this material has been prepared for a specific communication methods university course.

The examples presented in this paper are not from real studies, but specifically calculated for the purposes of the discussed themes, so they should not be taken as real research results. I have tried to avoid using any formulas and presented mathematical expressions only when I think it is absolutely necessary for the understanding of the explained matter. However, even then I have done so informally, with a focus on getting an intuitive grasp of the matter.

What will follow in this document is mainly based on my own experiences in teaching quantitative methods courses for communication students during three semesters. Hence, the choices made on what is included and excluded from the presentations of various methods are based on my comprehension of how much information is necessary for students whose background knowledge of statistics and research methods is not that strong yet. I have added a lot of links and options for further readings for those who would like to deepen their knowledge on some issues.

The presentations of issues and methods is not by any means meant to be exhaustive; rather the purpose has been to provide an easy and self-contained introduction to various options that are available if one chooses to conduct quantitative research. The focus will be heavily on the hands-on approach that I have adopted in my own studies of statistics and quantitative methods.

Please, download the whole document at here or browse the material online.