Eilisen syntymäpäiväni kunniaksi päätin tehdä syntymäpäiväaiheisen postauksen. Moni on ollut ehkä kuuntelemassa (tai katsonut videolta) puhujaa tai luennoitsijaa, joka kysyy, sattuuko kenelläkään yleisössä olemaan syntymäpäivä. Yleensä käsiä aina nousee pystyyn. Voi tuntua sattumalta, että jollakin on syntymäpäivä juuri sinä päivänä, kun sitä kysytään. Onkin kiinnostavaa, mikä on syntymäpäivän todennäköisyys eri kokoisissa yleisöissä. Tähän saadaan teoreettinen vastaus todennäköisyyslaskennan avulla.
Oletetaan, että kaikki syntymäpäivät ovat yhtä todennäköisiä (vaikka ne eivät ole), että niitä on yhteensä 365 kpl ja että syntymäpäivä ei vaikuta yleisön valikoitumiseen millään tavalla (vaihtele siis satunnaisesti suhteessa yleisöön). Tarkastellaan tilannetta, jossa vähintään yhdellä yleisön joukossa on syntymäpäivä. Syntymäpäivän todennäköisyys on 1/365 jokaiselle yleisön jäsenelle, ja todennäköisyys puolestaan sille, että henkilöllä ei ole syntymäpäivää on 364/365. Yleisöjoukon kaikkien mahdollisten alkeistapausten (mahdollisten syntymäpäiväyhdistelmien) määrä on 365 x 365 x 365 … n. Määritellään todennäköisyys “vähintään yhdellä on syntymäpäivä” vastatapahtuman “kenelläkään ei ole syntymäpäivä” avulla: P(vähintään yhdellä on syntymäpäivä) = 1 – P(kenelläkään ei ole syntymäpäivä). Koska yleisön koko on toistaiseksi rajoittamaton merkitään sitä n:llä. Siten:
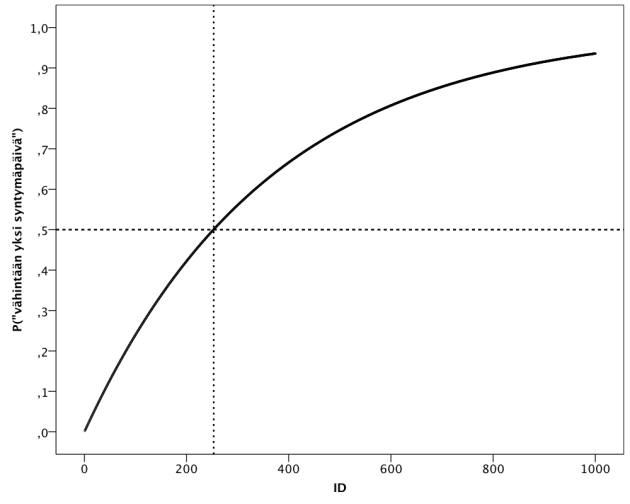
Nyt voidaan laskea esimerkiksi että jos n = 1000, niin P = 0.936, eli tuhatpäisessä joukossa vähintään yhdellä henkilöllä on syntymäpäivä jo 94% todennäköisyydellä. Otetaan SPSS avuksi ja tarkastellaan, miten yleisön koko vaikuttaa todennäköisyyteen onnistua löytämään syntymäpäiväsankareita. Luodaan aluksi 1000 havaintoa ja lasketaan sitten kullekin “yleisömäärälle” oma todennäköisyytensä. Piirretään tämän jälkeen nämä vastakkain.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
set seed = 100. input program. loop #i = 1 to 1000. compute ID = #i. end case. end loop. end file. end input program. dataset name birthday. execute.compute P_birthday = (1-(364/365)**ID). VARIABLE LABELS P_birthday 'P("vähintään yksi syntymäpäivä")'. execute.GRAPH /SCATTERPLOT(BIVAR)=ID WITH P_birthday. |
Kuvaajasta huomataan, että todennäköisyydet kasvavat yleisömäärän mukaan logaritmisesti. Kasvu on aluksi nopeaa ja sitten hidastuu kohti ääretöntä. Apuviivojen leikkauspisteestä voidaan poimia “kriittinen raja” sille, kannattaako temppua yrittää eli ovatko mahdollisuudet enemmän kuin fifty-fifty. Tuo raja on 253 yleisön jäsentä, eli tuota kokoa suuremmissa yleisöissä on todennäköisempää että vähintään yhdellä on syntymäpäivä kuin että kenelläkään ei olisi, ja kun n > 500 alkaa todennäköisyys olla jo melko korkealla (>75%). Sama raja voitaisiin tietysti laskea myös yllä esitetystä kaavasta ratkaisemalla n, kun kaavan arvoksi asetetaan 0.5:
PS. Todennäköisyyslaskennassa on esitetty pitkään hieman toisenlaista ja paljon yllättävämpää “syntymäpäiväongelmaa”, jossa etsitään sellaisen joukon kokoa, jossa todennäköisyys sille, että vähintään kahdella henkilöllä on sama syntymäpäivä olisi yli 0.5. Hämmästyttävästi tämä ehto täyttyy jo 23 ihmisen kokoisessa joukossa! Katso miten.
Postaus on julkaistu alun perin 6.11.2013.