Kurssi on edennyt sutjakkaasti ja nyt päästiinkin viimeisen harjoitustehtävän pariin. Valitettavasti työmäärä oli yllättäin aivan liian suuri ja jätti muuten niin kivaksi osoittautuneesta kurssista pahan maun suuhun. Interpoloinnit tuli kuitenkin opittua.
Interpoloinnilla useimmiten tarkoitetaan vektorimuotoisten pisteiden tiedon muuttamista rasterikartaksi. Kunhan pisteet ovat jotenkin spatiaalisesti autokorreloituneista, syntyneessä kartassa arvot vaihettuvat asteittain toisiksi. Tällaisia vaihettuvia pintoja vektorimuotoisina on hyvin vaikea tehdä, toisin kuin rasterimuotoisina.
Interpolointimenetelmiä on monenlaisia ja tässä harjoituksessa tutustuttiin muutamiin. Nämä ovat Thiessenin polygonit, trendipintainterpolointi, inverse distance weighted -interpolointi, spline ja muutama kriging-menetelmä.
Harjoituksessa neljä ensimmäistä interpolointia suoritettiin vuoden 2020 kuukausittaisilla lämpötila-aineistoilla Suomen sääasemilta. Aluksi suoritettiin nopea tietokenttäliitos. Tämän jälkeen muunnettiin tammikuussa mitattujen lämpötilojen arvot oikeasti numeromuotoisiksi luomalla uuden float-tyyppisen sarakkeen ja siirtämällä calculate fiedlillä arvot siihen. Nyt tammikuun lämpötila-aineisto oli siinä muodossa, että sitä saattoi lähteä interpoloimaan. Kopioitiin kartta, jolla tämä suoritettiin, viiteen työtilaan, joihin saatettiin lähteä tekemään eri analyyseja.
Aluksi interpoloitiin Thiessenin polygonit. Tämä menetelmä luo pisteiden ympärille polygoneja, joilla on sama arvo kaikkialla. Tämä ei varsinaisesti ole interpolointia, mutta ollessaan varsin kevyt analyysi, sitä voi hyödyntää nopeissa ja ei paljoa tarkkuutta vaativissa tilanteissa.
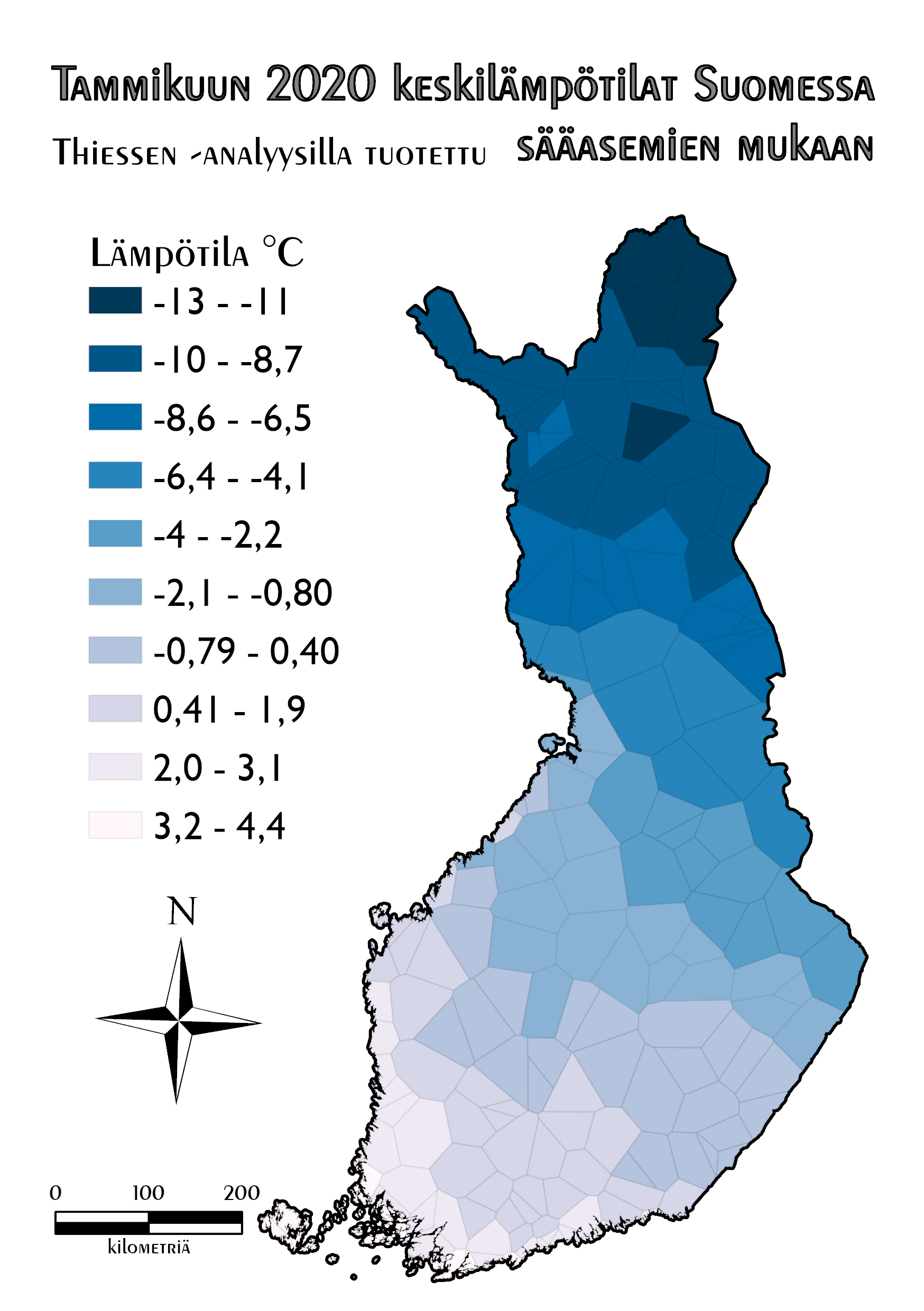
Lopputuloksesta (Kuva 1) näkyy selkeästi, miten lämpötilat laskevat pohjoiseen ja itään mennessä. Käytin visualisoinnissa natural breaks -luokittelutapaa ja hyvin kylmyyttä kuvaavia värejä.
Kuva 1. Thiessenin polygoneilla tehty interpolointi.
Seuraavana tutustumisvuorossa on trendipintainterpolointi. Kyseessä on Thiessenin polygonien tavoin deterministinen interpolointimenetelmä. Deterministiset interpolointimenetelmät perustuvat matemaattisiin funktioihin. Trendipintainterpoloinnissa funktiot ovat polynomifunktoita, joilla luodaan trendipinta pisteiden arvoilla.
Trendipintainterpolointi on myös globaali operaatio. Tämä tarkoittaa sitä, että pisteiden arvot vaikuttavat kaikkialla. Thiessenin polygonimenetelmä taas oli lokaali interpolointitapa, joissa pisteiden arvot vaikuttivat vain naapurustossaan.
Varmaankin juuri interpoloinnin globaaliuuden takia interpoloitava alue aluksi rajattiin hieman Suomen rajojen ulkopuolelle. Tämän jälkeen trendi-interpolointi suoritettiin kolme kertaa eri asteisina. Trendi-interpoloinnin aste kertoo kuinka monennen asteen polynomin mukaan interpolointi on suoritettu.
Tässä kohtaa huomaan jälkikäteen olleeni huolimaton. Huomasin kyllä interpolointeja suorittaessani, että kun niitä tekee kolmella kartalla samanaikaisesti, ArcGis pitää samoja asetuksia kaikilla välilehdillä. Näin tuli vahingossa interpoloitua monella kartalla kolmannen asteen trendillä jne. Jotenkin lopulliseen karttaesitykseen (Kuva 2) pääsi livahtamaan ensimmäisen ja toisen asteen interpolointiin sama kartta, vaikka olin varmasti tehnyt lopulta erikseen kolme eri asteen interpolointia eri kartoille.
Interpoloinnin jälkeen clip-työkalulla rajattiin ylimääräiset alueet pois. Tämä muutti visualisointitavan tretch-tyyppiseksi, jolloin arvot vaihtuisivat häilyen. Tämä on trendi-interpoloinnille ihan hyvä esitystapa, mutta tehtävän kannalta olisi tärkeää erottaa eri asteisten trendipintainterpolointien erot, joten päädyin lopulta classify-visualisointitapaan. Luokkia tein kymmenen niin erot erottuvat selkeästi, mutta luokat mahtuvat edelleen legendaan. Luokittelytapana equal interval.
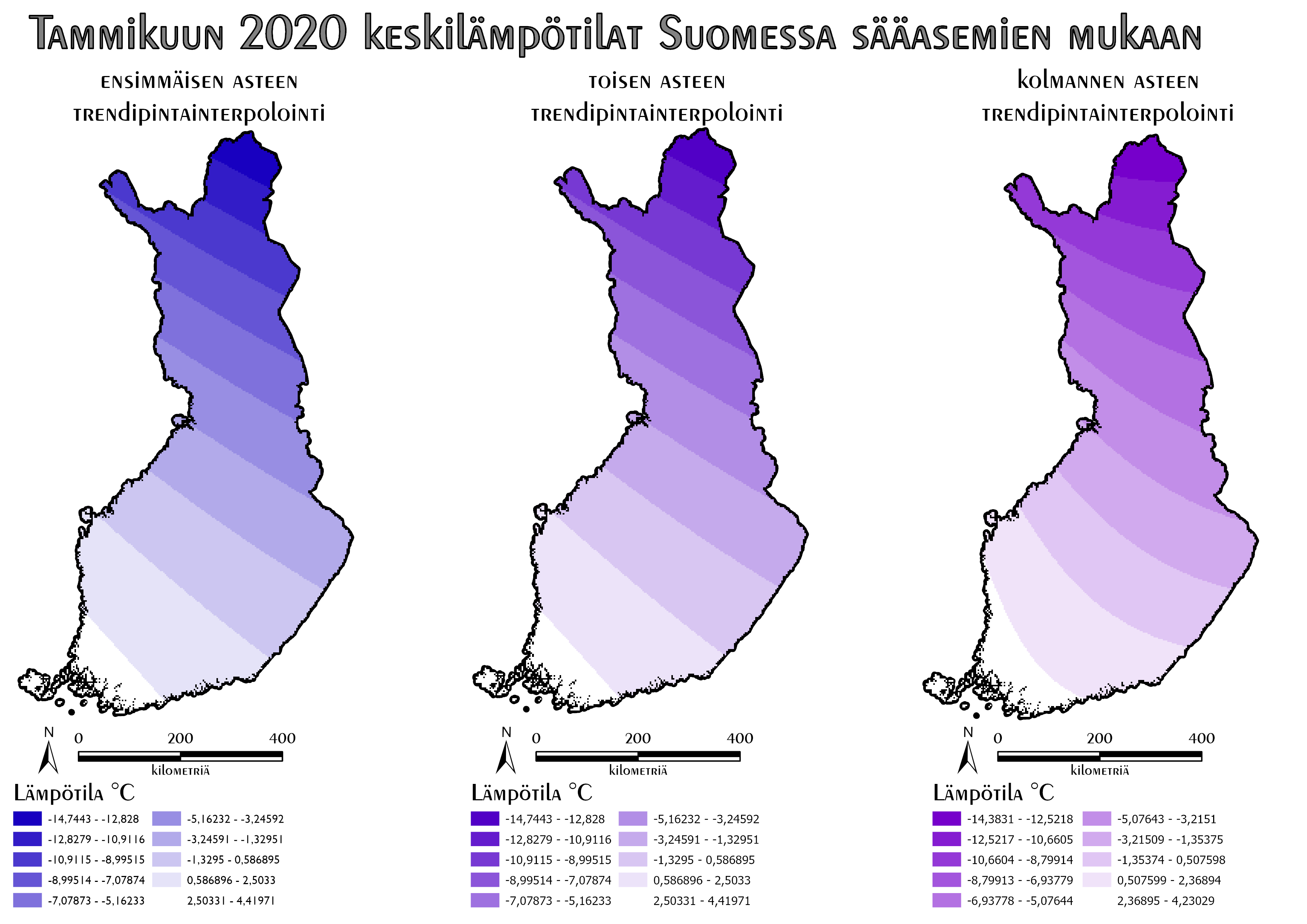
Ensimmäisen, toisen ja kolmannen asteen trendipintainterpolointeja verratessa (Kuva 2) huomaa, miten asteiden kasvaessa myös kaarevuus kasvaa. Legendassa myös luokkien koot eroavat hieman.
Trendipintainterpolointi antaa erittäin yleistetyn kartan, jolloin se sopii lähinnä suurpiirteisten ilmiöiden kuvaamiseen. Kartalta erotamme, että Lounais-Suomi oli tammikuussa 2020 lämpimin ja Pohjois-Lappi sekä käsivarsi kylmin, ja että lämpötila vaihettui tasaistesti siinä välillä. Tarkempia havaintoja tehdessä todennäköisyys virheisiin kasvaa.
Kuva 2. Ensimmäisen, ensimmäisen ja kolmannen asteen trendipintainterpolointi.
Seuraava deterministinen interpolointimenetelmä, Inverse Distance Weighted eli IDW suorittaa interpoloinnin deterministisesti huomioiden mm. pisteiden väliset etäisyydet, määrän ja keskiarvot.
Interpolointi suoritettiin Geostatistical Wizard -työkalulla. Tällä sai kokeiltua kätevästi eri arvoja ja asetuksia. Tavoitteena oli saada Root Mean Square ja Mean -arvot mahdollisimman lähelle nollaa sekä saada kaavion käyrät päälleekäin. Power-arvon optimointi tuotti edullisimmat tulokset. Optimoitu power-arvo on 3,05911429270362. Powerilla säädetään sitä, miten paljon paikalliset arvot ja muutokset vaikuttavat. Tämä on olennainen säätö IDW-interpoloinnissa. Muita muutoksia analyysiin en Geostatistical Wizardilla tehnyt. Neighbourhood typen ja Sector Typen muuttaminen kasvattivat Root Mean Squaren ja Meanin arvoja.
Interpoloinnin valmistuttua muutettiin tasoa GA Layer to Raster -työkalulla, missä oli jännä huomata muutoksia isaritmeissa. Clipattiin taas alueesta ylimääräiset pois tällä kertaa ilman tarkempia ohjeita. Ja onnistuihan se heti kun muisti ruksata ”Use Input Features for Clipping Geometry” -kohdan.
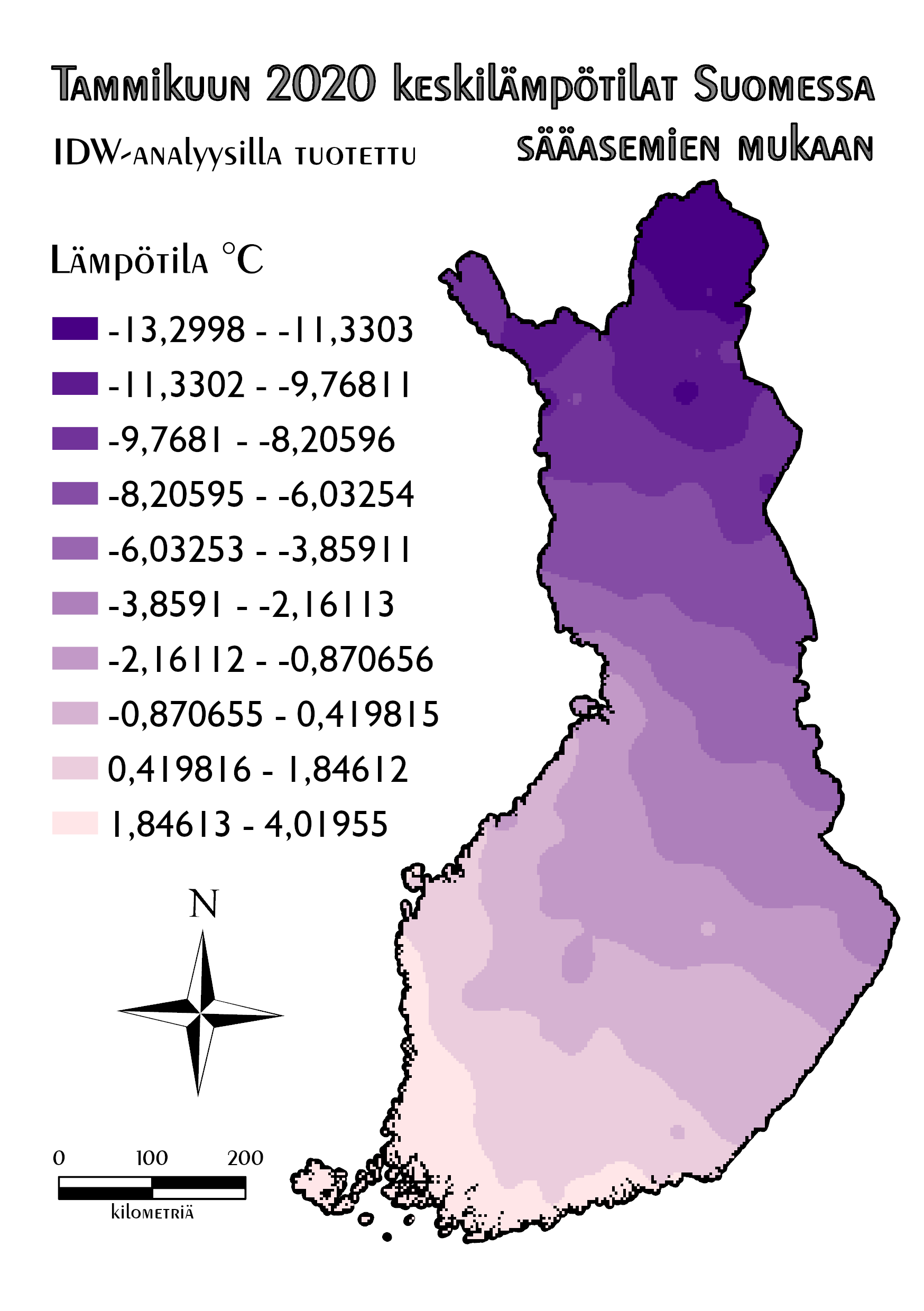
Visualisoinnissa päädyin taas kymmenen luokan classify -tapaan, vaikka stretch olisi nyt toiminutkin ihan hyvin. Stretchissä havaintoasemat näkyivät näppylämäisinä eroamina kartalla vielä selkeämmin kuin classifyllä. Lopputuloksessa (Kuva 3) jatkoin tämän kurssikerran siniviolettia väriteemaa.
IDW tuotti tähän mennessä ehkä tarkimman lämpötilakartan.
Kuva 3. Inverse Distance Weighted -interpoloinnilla tehty kartta.
Seuraavana kokeiluvuoron sai deterministinen spline-interpolointi. Tämä menetelmä luo samanarvokäyriä minimoiden pinnan kaarevuuden.
Tässä harjoituksessa tavoitteena oli tehdä jokaiselle kuukaudelle vuodelta 2020 oma lämpötilakarttansa. Tämä tapahtuisi ArcGissin ModenBuilderilla. Työkalun käyttö sujui hyvin, olihan se tuttu jo edellisviikon harjoituksesta.
Apply symbology from layer -valikosta en löytänyt tmluokat.lyr -vaihtoehtoa, koska tehtävässä ei koskaan pyydetty sitä lisäämään projektiin. Lisäsin sen visualisoidessa import from layer file -kohdasta.
Tappelut karttojen symbologian kanssa saivat hermoni kiristymään edelleen tämän loputtoman tehtävän kanssa, joten päätin tämän tehtävän kanssa vähän oikaista ja tein vain kaksi kuukautta kahdentoista sijaan.
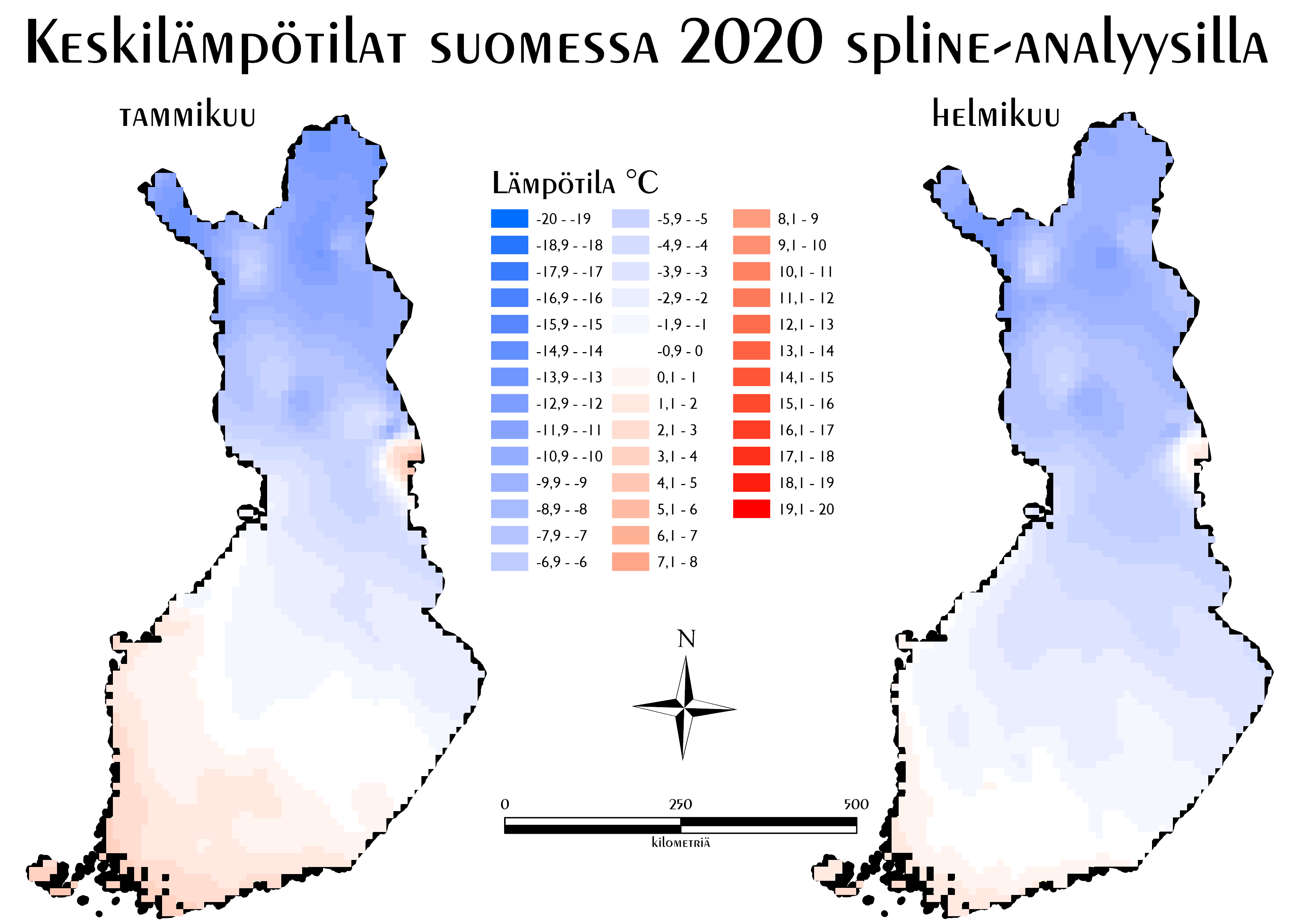
Kuvassa 4 on lopulliset tekemäni spline-interpolointikartat. Visualisoinnissa on enemmän luokkia kuin aiemmissa interpoloineissa, joten tulos näyttää automaattisesti paremmalta. Sanoisin kyllä muutenkin, että kyseinen interpolointi sopii tarkkuudessaan aika hyvin juuri tähän lämpötilojen interpolointiin.
Kuva 4. Spline-interpoloinnilla tedyt kartat.
Tässä olivat tässä harjoituksessa läpikäytävät deterministiset interpolointimenetelmät. Lämpötilakartoille paras interpolointimenetelmä on mielestäni spline, mutta IDW toimi myös hyvin. Lämpötiloja esitettäessä ollaan yleensä kiinnostuneita tietyn alueen tai pisteen lämpötiloista, joihin edellä mainitut sopivat. Trendipintainterpolointi yleisti todella paljon, joten se sopisi suuren mittakaavan ilmiöihin ja thiessenin polygonit taas toimivat parhaiten, jos on todella paljon havaintopisteitä sekä niiden välisiä eroja, jotka saavat näkyä.
Seuraavaksi siirrytään determiistisistä interpolointimenetelmistä geostaattisiin. Matemaattisten funktioiden sijaan geostaattiset interpoloinnit suorittavat laskelmat tilastollisesti. Tässä harjoituksessa käytettävä kriging-interpolointi huomioi spatiaalisen autokorrelaation.
Aluksi kokeiltiin Simple Kriging -interpolointia. Analysoitavana on pääkaupunkiseudun ilman typpioksidipitoisuudet. Arvoja tarkasteltiin histogrammissa, mistä kävi ilmi, ettei kyseessä ole normaalijakaumaa. Ilmanlaadultaan huonoimmat, eniten typpioksidia ilmassa pitävät tutkimuspisteet löytyivät Sörnäisistä ja Esplanadin puiston länsikulmalta Helsingin keskustasta. Parhaan ilmanlaadun mitanneita pisteitä on seitsemän; kolme Espoossa Länsiväylällä, yksi Espoossa Luukissa, yksi Helsinki-Vantaan lentokentän tuntumassa, yksi Itä-Helsingissä ja yksi Pirkkolassa. Helsinki-Vantaalla oli oikeastaan kaksi hyvän ilmalaadun mitannutta pistettä, mutta toinen osui pk-seudun rajan toiselle puolen.
Interpolointi tehtiin taas Geostatistical Wizard -työkalulla. Seurasin sokeasti vain ohjeita, että saisin tämän joskus valmiiksi.
Uudempi ja edistyneempi kriging -interpolointimenetelmä on Epieical Bayesian Kriging. Tämä jakaa aineiston osiin useita kertoja luoden aina useita semivariogrammeja. Näin saadaan aikaan tarkka spatiaalinen rakenne.
Interpolointi sujui mutkitta ohjeita seuraten. Interpolointitulos muutettiin rastereiksi levittäen sen koko pk-seudulle, jolloin simple krigingin tulos teki jänniä piikkimäisiä alueita, mutta ne saatiin siivottua visualisoinnissa.
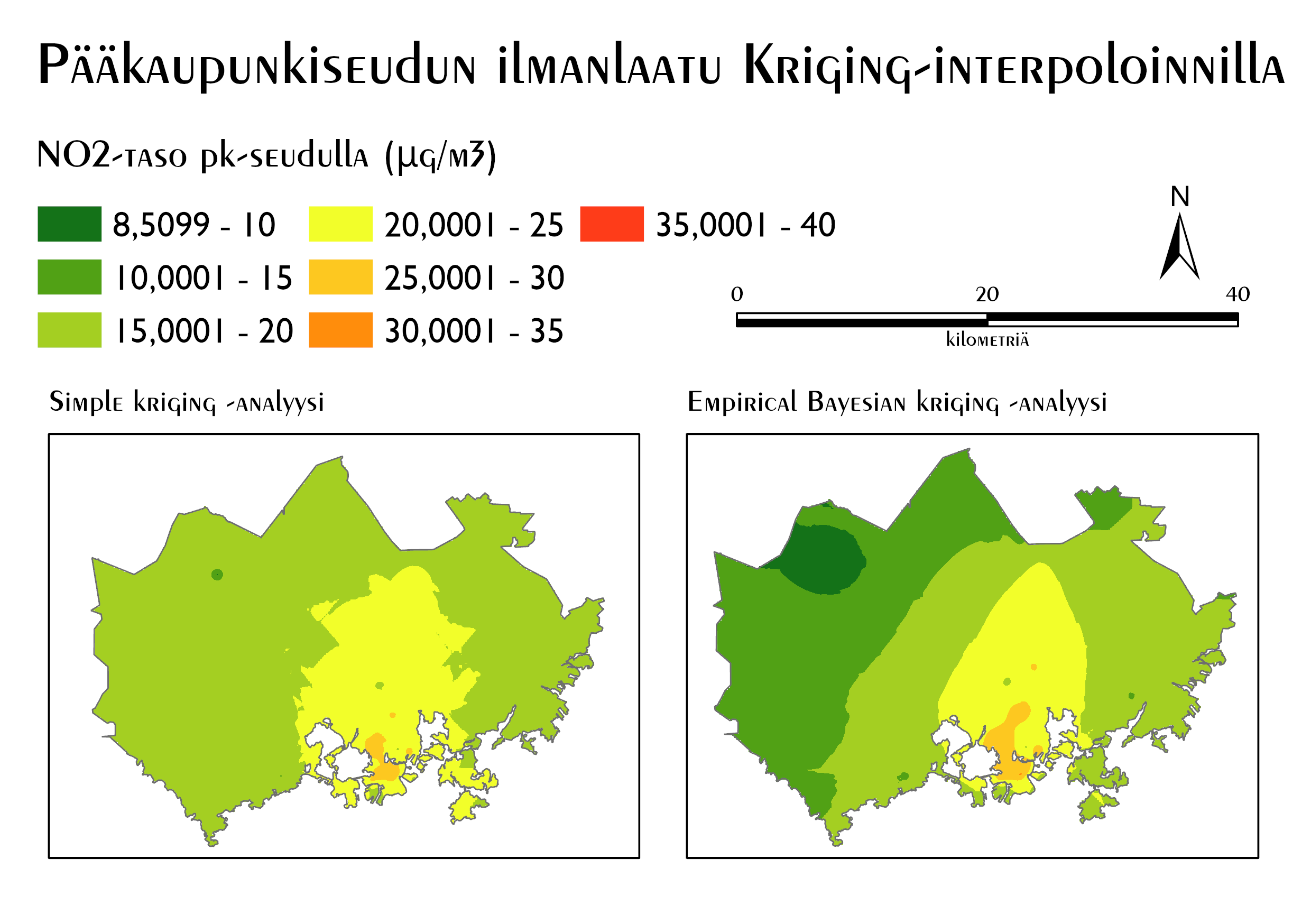
Interpolointien lopputuloksessa (Kuva 5) näkyy selkeä ero Simple Krigingin ja Empirical Bayesian Krigingin välillä. Jälkimmäisessä on pienimpien pitoisuuksien alueita paljon enemmän ja alueiden rajat ovat siistimpiä. Molemmissa kuitenkin selkeästi Helsingin keskustassa ja Länsiosissa ilmanlaatu on huonompi ja Espoossa taas kaikkialla laatu on parempi. Lähtöaineistossa saattaa olla jotain virheitä, sillä kartoilta on erotettavissa erillisiä pieniä plänttejä, joiden typpioksidipitoisuus eroaa ympäristöstä.
Kuva 5. Kriging-interpoloinnilla tehdyt kartat pääkaupunkiseudun eli Espoon, Kauniaisten, Helsingin ja Vantaan ilman typpioksidipitoisuuksista.
Pitkän puurtamisen jälkeen tämäkin raportti on viimein valmis. Harjoitustehtävään upposi todella paljon aikaa ja hermot kireänä harjoituksen koko loppupuoli syntyi hätiköiden ja mutkia suoristaen. On päivänselvää, että tämän viikon tehtävä oli aivan liian työläs. Kaikesta kuitenkin selvittiin aikarajoja venyttäen. Toivottavasti tämä arvioidaan vasta tammikuun puolella.
Interpoloinnit olivat kuitenkin ihan jänniä ja kivoja. Varmasti tulen näitä tällä kurssikerralla oppimiani asioita vielä hyödyntämään myöhemmin.