𝛑 appears in most non-expectable math identities.

In 1689, famous swiss professor Jakob Bernoulli paid attention to a quite specific mathematical problem, which is sum of infinite reverse squares, today it is known as Basel problem. Although formulation itself sounds a bit fancy for non-mathematician, it is just summation of series where 1 is divided by number squared:

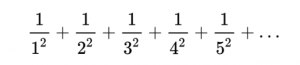
Not too complicated if you managed to pass school math, but in the 17th century without calculators and computers, and limited knowledge about series it could take a while to find out the solution, especially considering that numbers go on to infinity…

 

46 years later, in 1735 swiss mathematician Leonard Euler was able to find out that infinite sum of reverse squares equals 𝛑2/6. Wow! Why would 𝛑 appear somewhere else than in circle area? Although Euler himself used very complicated math, proving this identity can be understood even by 9th graders, and yes, it involves circles. 

 

So why would 𝛑 appear in such non-related to geometry problem? Let’s find out!

 

Inverse squares appear in physics, in fact, if you imagine a light source at a distance one unit from you, the brightness received by your eye would be 1, but if it is at a distance two units away, you would see only one fourth of the original brightness. Hence, at distance three you see only one ninth of original brightness, this comes from properties of light and other physical quantities such as heat, sound, radio waves and etc. We can already see what are next steps… In the theoretical approach Basel problem can be represented within physical objects. 

 

But how can we manipulate our light sources to understand the math behind? 

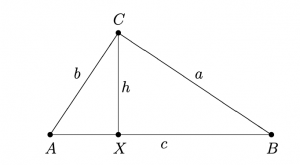
It would be quite easy, in the picture above imagine yourself standing at point C, and the light source would be on point X. Due to properties of Pythagorean theorem (its inverse to be precise), the brightness received by your eyes from light source at point X would be the same if there were two same light sources at points A and B. Therefore we can “exchange” one light source to two other similar ones which lie on the apex of the right triangle. 

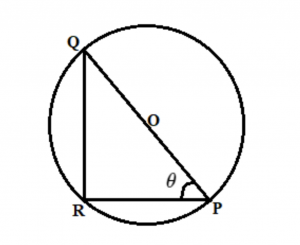
To refresh school memory, I remind you that if one of triangle’s side is circle’s diameter, and the third apex is on the side of circumference, than it would always be right triangle with perfect 90 degree angle. 

 

Can you already see where it is going? =) 

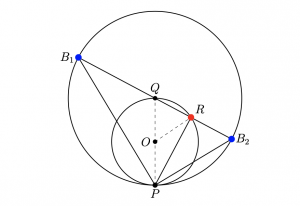
If you imagine yourself standing on point P and your light source is on point Q, where PQ is the diameter of a circle, it would be the same physical picture in terms of brightness received by your eye if there was a circle twice as big and there were two light sources on sides of a bigger circle. And we can keep adding light sources on the sides of a circle which is twice bigger until we end up standing on the edge of a circle of infinite circumference with the same brightness received by our eyes! 

 

Now, back to school geometry, consider that length of a circumference is 2𝛑r, and all over the circle on same evenly spaced distance there are our light sources which appear with same brightness to our eyes, but each would be in the inverse distance squared. Simple algebraic manipulations lead to the final cut: adding inverse squares up to infinity comes up to be… 𝛑2/6! Boom!

 

Knowing the properties of physical quantities, light in our case, and simple Euclidean geometry can help us to prove the Basel problem without too complicated formulas. 

 

In fact, there are tonnes of other modern methods to prove Basel problem, for example some other way would look something like this:

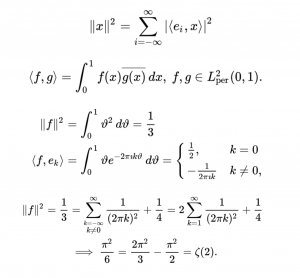
Too bad those guys did not pay attention in their geometry lessons in 8th grade!

Based on: No. 524 (July 2008), pp. 313-316 Johan Wästlund, “Summing inverse squares by euclidean geometry” http://www.math.chalmers.se/~wastlund/Cosmic.pdf

Filipp Volodin