Can patterns solve an unsolvable puzzle?

Are you a fan of puzzles? Perhaps riddles are more your style. Maybe you are someone who is partial to the occasional thought experiment. Regardless, chances are the highlight of a puzzle is finding the solution. Unfortunately, this is something that is not always so straightforward when maths gets involved.

 

The Collatz conjecture, invented by Lothar Collatz, has been around since 1937. To this day it is incredibly famous, all because it has been so difficult to solve. 

 

At first glance it may appear simple, it goes as follows: 

 

Take any whole number.

 

If it is even, half it.

 

If it is odd, multiply by 3 and add 1.

 

This process is repeated indefinitely, causing a sequence of numbers to form. 

 

This doesn’t seem all too complicated from a mathematical standpoint; in fact, it would be pretty easy to do this yourself (perhaps with a calculator when the numbers get very big). So why has it had mathematicians stumped for so many decades? 

 

So far, every number tested falls into the loop of 4 then 2 then 1. This becomes an infinite loop since 1 is odd so would be used in the 3n+1 function, which will give the output 4. 4 is even so it is halved to give 2. 2 is also even so it is halved again, and we are back at 1, only for it to loop back around again to 4. Mathematicians have spent decades trying to determine if every sequence will eventually reach this 4, 2, 1 loop for every single starting integer or if there is some whole number out there that produces a different result. The Collatz conjecture would be considered solved when it has either been proven to always reach the aforementioned loop or a contradiction has been found wherein this loop doesn’t occur.

 

Of course, being so old, many people have attempted to prove the Collatz conjecture, all without success! So maybe it’s time for some new ideas. 

 

The purpose of the article that I read was to approach the Collatz conjecture from a different perspective. It was all about clustering (plotting the various results onto a graph and examining how they group together). Clustering is something that I think shows a lot of promise when it comes to finding a proof. This is where the distance between the outputs is mapped onto a 3-dimensional chart. The distances are calculated using different Multidimensional Scaling algorithms where each equation examines something different. For example, the Hamming distance calculates to what extent components are identical or distinct while the Lorentzian distance compares small and large values using logarithmic functions.

 

As this is done over and over, different patterns start to form all depending on what distances are used. 

 

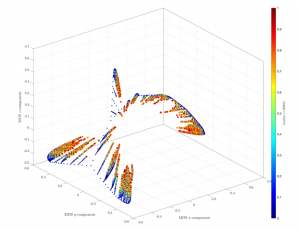
This example uses the ArcCosine-Hamming distance.

 

The idea here is to either spot clear outliers or clear patterns. Up until this point mathematicians have tried to prove the conjecture with computer programs that have tested it to ridiculously large numbers (2 to the power of 68, to be precise) or rigorous mathematical proofs. This is all great, but it lacks creativity which I think clustering brings. Every distance tested in the article showed an obvious pattern. From this it is made clear that displaying it visually and interpreting what we see rather than just relying on numbers can bring a whole new perspective to the problem.

 

In the end, this didn’t bring us to a solution but is definitely worth some merit and I don’t think it should be dismissed as a possibility any time soon.

 

Sometimes a logical problem requires an artistic solution.

 

Machado, José A. Tenreiro, Alexandra Galhano, and Daniel Cao Labora. “A Clustering Perspective of the Collatz Conjecture.” Mathematics (Basel) 9.4 (2021): 314–. Web.