Tekijä: Deleted User

Lukuvuosi on kohta aluillaan ja toista vuotta pitkää matematiikka lukevat ovat aloittamassa derivaattakurssia MAA6. Kisallioppiminen.fi:ssä rupeaa myös MAA6-kurssimateriaalin ensimmäinen versio olemaan valmis. Voi olla, että viimeisten lukujen kaikki tehtävät eivät ole ihan vielä kohdillaan ensimmäisen jakson alussa, mutta ne valmistuvat kyllä siihen mennessä, kun ne tulevat opiskelijoille ajankohtaiseksi.

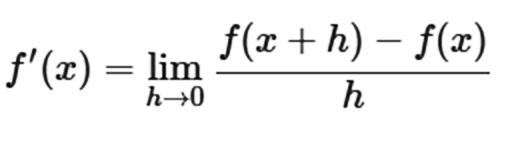
Kurssimateriaalin liittyy myös mukava yllätys, josta alla:

Stanfordissa vaikuttava matemaatikko Keith Devlin on yksi tunnetuimpia matematiikan popularisoijia. Hän on kirjoittanut matematiikan ideoista ja henkilöistä kirjoja, kehittänyt mobiilipelejä, kehittänyt verkkokursseja ja kirjoittaa blogeja.

Massiivisten avointen verkkokurssien -hypen ollessa kuumimmillaan 2012 hänen kurssialusta Courserassa tarjoamansa kurssi Introduction to Mathematical Thinking oli yksi edistyksellisimmistä kursseista. Kurssi pohjautui samannimiseen kurssiin, jota hän luennoi Stanfordin yliopistossa. Se keskittyi avartamaan osallistujien matemaattista maailmankuvaa, jonka koulumatematiikka oli saattanut surkastuttaa mekaaniseksi ulkoaopeteltujen algoritmien suorittamiseksi. Jotakin vastaavaa lukioon mukautettua sisältöä toivoisin jatkossa, kun pohditaan minkälainen MAY1-kurssin tulisi olla. Courserassa tarjotaan edelleen tätä kurssia, mutta Devlinin mielestä vesitettynä versiona.

Devlinin blogi Devlin’s Angle on mielestäni yksi parhaista matematiikkaa käsittelevistä blogeista. Muun muassa kertolaskua käsittelevät kirjoitukset It Ain’t No Repeated Addition ja It’s Still Not Repeated Addition aiheuttivat aikanaan paljon keskustelua. (Älkää antako vanhojen kirjoitusten ulkoasun rikkoutumisen vaivata, sillä sisältö on edelleen kohdillaan.)

Mielestäni yksi hienoimmista Devlinin kirjoituksista on vuodelta 2006,  Letter to a calculus student. Siinä Devlin kirjoittaa lyyrisesti ja vaikuttavasti differentiaalilaskentaa opiskelevalle opiskelijalle sen ideoiden kauneudesta. Usein matematiikan popularisoinnissa keskitytään matemaatikon (usein omaleimaisen) persoonan kuvailemiseen tai kuvataan matemaattisen idean sovelluksia. Kun matematiikan kauneudesta kirjoitetaan, esitetään usein geometrisia kuvia tai psykedeelisiä fraktaaleja. Devlinin tekstissä kuitenkin itse matematiikka on keskiössä. Tekstin lopetus on puhutteleva: ”If ever any painting, novel, poem, or statue can be thought of as having a beauty that goes beneath the surface, then the definition of the derivative may justly claim to have more beauty by far”.

Saimme Keith Devliniltä luvan suomentaa ja julkaista hänen blogikirjoituksensa kisallioppiminen.fi-sivulla ja Kirje differentiaalilaskennan opiskelijalle löytyy nyt MAA6-kurssin etusivulta. Olemme tästä hyvin kiitollisia ja toivottavasti sen lukeminen avartaa jollekin lukion opiskelijalle matemaatiikkaa uudella tavalla!

 

Thomas

Kisallioppiminen.fi-sivuille haluttiin luoda palvelu, jonka avulla opettaja pystyy seuraaman opiskelijoiden edistymistä ja opiskelijat välittämään tietoa siitä miten he kokevat hallitsevansa tehtäviä. Palvelua lähdettiin kehittämään Helsingin yliopiston tietojenkäsittelytieteen laitoksen opiskelijoiden voimin. Projektitiimin työnjälki on ollut todella huikeaa ja palvelu on nyt beta-testattavana osoitteessa http://beta.kisallioppiminen.fi.

Vaikka jakso olisi jo alkanut ja opiskelijat olisivat jo edenneet kurssilla, on kurssipalvelun käyttöönoton työmäärä niin pieni, ettei se estä beta-version kokeilua.

Alla on pikaohje palvelun käyttöönottoon. Kaikkea palautetta otetaan mielellään vastaan kommentteina, Facebookissa ja sähköpostitse.

Rekisteröityminen palveluun

• Palvelu edellyttää opettajalta ja opiskelijoilta Google-tunnuksia, joilla rekisteröidytään palveluun.
• Palveluun rekisteröidytään osoitteessa http://beta.kisallioppiminen.fi painamalla kirjaudu-nappia. Rekisteröitymisen yhteydessä palvelu saa tiedon käyttäjän nimestä ja sähköpostiosoitteesta. Muita tietoja ei kerätä eikä palvelua varten tarvitse luoda omia tunnuksia.
• Palvelun käyttöehdot:  https://github.com/kisallioppiminen/kisallioppiminen.github.io/blob/master/kayttoehdot.md

Kurssin luonti

Rekisteröinnin jälkeen voit luoda kurssihallinta-sivulla uuden kurssin jolla on kurssiavain:

Kun päivität Kurssihallinta-sivun, sivulle ilmestyy tekemäsi kurssi ja sen avain näkyy otsikossa. Painamalla kurssin otsikossa nuolta näet kaikki kurssin tehtävät.

Kun opiskelijoita liittyy kurssille ja he rupeavat tekemään tehtäviä, näet heidän edistymisensä paneelissa:

Kun liikutat hiirtä ruutujen päällä, näet mistä tehtävästä ja kenen vastauksesta on kyse.

Kurssille ilmoittautuminen

Omat kurssit -sivulta voit ilmoittautua kurssille opettajan antaman kurssiavaimen avulla. Kurssin opettaja ei voi liittyä kurssinsa opiskelijaksi.

Opiskelijana kurssilla

Kun opiskelija menee ilmoittautumisen jälkeen kurssille ja avaa tehtävän voi hän valita kolmesta hymynaamasta:

1. En osannut tehtävää. Tarvitsen apua.
2. Ratkaisin tehtävän, mutta olen epävarma vastauksesta.
3. Ratkaisin tehtävän ja osaan tämän.

Kun opiskelija valitsee jonkin vaihtoehdon, tehtävän otsikko muuttaa väriä. Opiskelija voi jälkeenpäin muuttaa vastaustaan.

Opiskelija näkee myös omat merkintänsä Omat kurssit -sivulta.

Hyvää pääsiäistä!

Thomas

Edit 13.4.2017: Lisätty kuva ja teksti opiskelijoista kurssilla.

Kokemuksemme mukaan vektoreita käsittelevä kurssi on monille opiskelijoille hankala. Kun ryhdyimme suunnittelemaan kisällioppimiseen soveltuvaa materiaalia, oli tavoitteenamme tehdä tästä kurssista entistä helpommin omaksuttava. Lisäksi halusimme tukea opiskelijoiden omaa ajattelua sekä tuoda esiin matematiikkaan kuuluvaa luovuutta. Seuraavissa kappaleissa kerron hiukan tarkemmin siitä, miten pyrimme toteuttamaan näitä tavoitteita. Materiaalin tämänhetkiseen versioon voit tutustua täällä.

Konkreettisesti koordinaatistossa

Materiaalin ensimmäisessä luvussa vektorit esitellään nuolina tasokoordinaatistossa. Tällä tavalla saadaan yhteys uuden käsitteen eli vektorin ja aiemman tiedon eli koordinaatiston välille. Toinen linkki uuden ja vanhan välillä on kirjaimilla laskeminen. Kun tasovektorit ilmaistaan koordinaattiakselien suuntaisten yksikkövektoreiden i ja j avulla, voidaan niiden yhteen- ja vähennyslasku sekä skalaarilla kertominen tehdä normaalin kirjainlaskennan tapaan.

Koordinaatisto sekä kantavektorit i ja j tuovat vektorin käsitteeseen paljon konkretiaa: vektoreita voidaan havainnollistaa piirtämällä ja niiden ominaisuuksia voidaan päätellä piirrosten avulla, mutta piirrosten tukena voidaan käyttää myös laskuja. Piirtäminen on erityisen tärkeää silloin, kun vektorin käsite on vielä uusi, sillä näin opiskelijoille muodostuu oikeanlaisia mielikuvia siitä, mitä erilaiset vektoreihin liittyvät käsitteet tarkoittavat. Nämä mielikuvat auttavat ongelmien ratkaisemisessa myös myöhemmin, kun tilanteet muuttuvat abstraktimmeiksi.

Lukion oppikirjoissa vektorin käsite on yleensä tapana määritellä suunnan ja suuruuden käsitteiden avulla. Tässä suhteessa materiaalimme siis poikkeaa perinteestä. Vektori on kuitenkin hyvä esimerkki käsitteestä, jonka määritelmä vaihtelee sen mukaan, millä matematiikan tasolla liikutaan. Korkeakoulumatematiikassa vektorit voidaan määritellä aluksi lukupareina, sitten lukukolmikkoina ja (äärellisinä) lukujonoina, myöhemmin abstraktisti minkä tahansa vektoriavaruuden alkioina.

Mainiot mallikuvat

Kun kaikki vektoreihin liittyvät peruskäsitteet ja laskutoimitukset ovat tulleet tutuksi tasokoordinaatistossa, siirrytään materiaalin toisessa luvussa avaruuskoordinaatistoon. Samalla piirtämisessä siirrytään astetta abstraktimmalle tasolle ja aloitetaan mallikuvien piirtämisen harjoittelu. Piirtäminen on siis edelleen tärkeässä roolissa, mutta myös laskennallisten perusteluiden paino kasvaa. Vektorien yhdensuuntaisuuden tutkiminen johtaa yhtälöryhmän ratkaisemiseen. Kahden ja kolmen tuntemattoman yhtälöryhmiä opetellaan ratkaisemaan sijoitusmenetelmällä, ja tätä taitoa käytetään myös vektorin jakamisessa komponentteihin.

Materiaalin loogisesta rakenteesta on pyritty tekemään mahdollisimman selkeä ja matematiikkaa tieteenalana kuvaava. Vihertävällä pohjalla olevat määritelmät ovat sopimuksia siitä, mitä jollakin käsitteellä tarkoitetaan. Harmaalla pohjalla olevat teoreemat puolestaan ovat matemaattisia tosiasioita, jotka voidaan perustella todeksi määritelmien pohjalta. Osa ensimmäisessä luvussa esitellyistä teoreemoista perustellaan luvussa 2, jolloin niiden sisältö on tullut jo tutuksi soveltamisen kautta.

Sovelletaan suoriin, treenataan tasoilla

Materiaalin kolmannessa luvussa pysytellään edelleen kaksi- ja kolmiulotteisissa koordinaatistoissa. Edellisissä luvuissa opittuja asioita päästään nyt hyödyntämään, kun suorien ja tasojen ominaisuuksia tutkitaan vektoreiden avulla. Suoria tarkastellaan ensin tasokoordinaatistossa, jossa havainnollistaminen ja oikeiden mielikuvien luominen tarkkojen kuvien avulla onnistuu. Avaruuskoordinaatiston suorista ja tasoista piirretään mallikuvia.

Matematiikkaan kuuluvaa luovuutta tuodaan materiaalissa esiin tehtävissä, joissa opiskelijat saavat itse keksiä esimerkkejä. Opiskelijoiden omaa ajattelua tuetaan lisäksi tehtävillä, joissa opiskelijaa pyydetään selittämään omin sanoin havaintojaan ja ratkaisutapojaan, sekä tehtävillä, joissa tuloksen järkevyyttä pitää arvioida esimerkiksi piirroksen avulla.

Huomaamaton huipennus

Neljännessä eli viimeisessä luvussa ratkaistaan geometrisia ongelmia ilman koordinaatistoa. Taso- ja avaruuskoordinaatistoissa harjoiteltu vektoreiden laskutoimitusten geometrinen tulkinta on keskeisessä asemassa. Tavoitteena on, että opiskelijoilla on tässä vaiheessa vahva rutiini mallikuvien piirtämiseen, jolloin koordinaatistosta luopumista ei välttämättä edes sen suuremmin huomata.

Kisällioppimisen menetelmässä korostuu opiskelijoiden oma aktiivinen tiedon prosessointi. Materiaalissa tätä tuetaan tehtävillä, jotka nivoutuvat oleelliseksi ja erottamattomaksi osaksi teoriaosuutta. Uudet asiat havainnollistuvat näiden tehtävien kautta pienin askelin. Oman työn ja osaamisen arviointia harjoitellaan jokaisen luvun lopussa itsearvointitestien avulla. Näin opiskelijat saavat jatkuvaa palautetta oppimisestaan paitsi oppituntien aikana ohjaavalta opettajalta, myös tuetun itsearvioinnin kautta.

Opetushallitus teki pienen killerin uuteen lukion opetussuunnitelman perusteeseen (OPS). Vanhan OPS:n löysä “opetus pyrkii myös antamaan opiskelijalle selkeän käsityksen matematiikan merkityksestä yhteiskunnan kehityksessä” (korostus oma) on edelleen jäljellä, mutta pitkän ja lyhyen matematiikan yhteiseen MAY1-kurssiin on pistetty ensimmäiseksi tavoitteeksi, että opiskelija “pohtii matematiikan merkitystä yksilön ja yhteiskunnan näkökulmasta”. Kurssin keskeinen sisältö on täysin matemaattinen, joten mitä tästä oikein pitäisi ajatella?

Kurssihan on koko uuden OPS:n suurin muutos matematiikan osalta ja sen kurssimateriaalin pähkäily ei ole ollut tässäkään projektissa ihan yksinkertaista. Mutta työpaikalle pyöräillessäni ajatukseni harhaili tuohon ensimmäiseen tavoitteeseen: “Pohtii matematiikan merkitystä…”. Onneksi siinä ei sanota “Ymmärtää matematiikan merkityksen yhteiskunnalle ja yksilölle”, koska se vaatisi vähintään matematiikkaa, yhteiskuntaoppia, historiaa, filosofiaa ja kaikkia luonnontieteitä yhdistävän monumentaalisen teemaopintokurssin.

Jos lähdetään siitä, että opiskelijoiden olisi hyvä elämässään edes kerran pohtia matematiikan merkitystä yhteiskunnalle ja yksilölle ja aikaa siihen olisi vaikka yksi oppitunti, niin miten heitä evästäisi pohdinnoissa?

Joo tiedän – tähän voisi suhtautua siten, että tulipahan taas keskusvirastosta määräys, joten pohditaanpa nyt kymmenen minuuttia matematiikan merkitystä: “Sofia, mikä on sinusta matematiikan merkitys yhteiskunnassa?”, “No, ilman matematiikkaa meillä ei olisi mobiiliteknologiaa, koska siinä käytetään koko ajan matematiikkaa.” “Hyvä Sofia. Mites Elias, mikä on sinun mielestäsi matematiikan merkitys yksilölle?”, “No, ymmärrän ainakin vähän millainen asuntolaina minun kannattaa ottaa”. “Tosi hyvä Elias. Onpahan nyt pohdittu hyvin. Siirrytäänpäs sitten matematiikkaan ja lukujonoihin…”.

Oikeasti näiden asioiden pohtiminen on mielestäni mitä hienoin tavoite. Toivottavasti opiskelijat menisivät pohdinnoissaan joitakin ilmeisiä yksittäisiä matematiikan sovelluskohteita pidemmälle.

Rupesin miettimään, voisiko pohdinnan aloittaa siten, että mitä jos ihmiskunta ei olisi kyennyt kehittämään matematiikkaa. Tilanne olisi sama kuin jos ihmiskunta ei olisi kyennyt kehittämään luku- ja kirjoitustaitoa. Eloonjäämisen kannalta nämä eivät ole välttämättömiä taitoja – säilyiväthän ihmiset hengissä ennen kuin sumerialaiset kehittivät nuolenpääkirjoituksen, mutta aika kivikautinen meidän yhteiskuntamme olisi ilman luku- ja kirjoitustaitoa. Tässä voisi olla opiskelijoilla pohdittavaa.

Toisaalta matematiikan sanotaan usein kehittävän ajattelun taitoja. Näinhän asian laita tietenkin on, mutta mielestäni siinä olennaista on nimenomaan se, että se harjoittaa ajattelun taitoja. Näitä matemaattisen ajattelun osa-alueita ovat esimerkiksi aritmeettinen, geometrinen, algebrallinen ja laskennallinen tai algoritminen ajattelu, joista viimeistä harjoitellaan perusopetuksessa syksystä 2016 lähtien ohjelmointia opettelemalla.

Ajattelin, että yksi konkreettinen esimerkki yläkoulusta on Pythagoraan lause, joka ilmiselvien sovellusten lisäksi myös voisi johdattaa opiskelijat pohtimaan todistamista ja sitä ettei kaikkia matemaattisia ongelmia ole vielä ratkaistu. Minusta olisi hyvä, että opiskelijat näkisivät matematiikan kehittyvänä tieteenä eikä vaan staattisena monoliittina, niinkuin se kouluopetuksessa helposti näyttäytyy.

Tein ajatuksistani version luvuksi MAY1-kurssiin otsikolla “Matematiikan merkityksestä yhteiskunnalle ja yksilölle” (avautuu klikkaamalla otsikkoa), johon mielelläni ottaisin kommentteja. Erityisesti tehtävät mietityttävät.

Ensimmäistä ylppärikoetehtävää aiheesta odotellen.

Thomas

Tässä blogissa voi seurata, miten tehostetun kisällioppimisen menetelmää toteutetaan lukiossa. Avaamme tässä ensimmäisessä kirjoituksessa, mistä kisällioppimisessa on kyse.

Modernit tulkinnat kisällioppimisesta syntyivät 80-luvulla, kun ruvettiin tutkimaan, miten perinteisissä käsityöammateissa käytettyjä oppimisen menetelmiä voitaisiin soveltaa formaalissa kouluopetuksessa opetettaviin sisältöihin kuten matematiikkaan, lukemiseen ja kirjoittamiseen. Muun muassa näihin ajatuksiin perustui uusi näkökulma oppimiseen, jossa korostettiin oppimistilanteen merkitystä oppimisessa ja ennen kaikkea sitä, ettei oppimistilannetta voi erottaa opetettavasta sisällöstä. Esimerkiksi jos matematiikkaa opetetaan luennoimalla, niin oppilas ei ainoastaan opi opettajan esittelemää tietosisältöä, vaan oppimistilanteen myötä myös sen, että matematiikkaa opitaan kuuntelemalla opettajaa. Myös ne oppilaat, jotka eivät opi opettajan esittelemiä tietosisältöjä, oppivat koko ajan – he oppivat, että eivät ole hyviä matematiikassa, että matematiikka on tylsää, että tärppejä ulkoalukemalla pääsee kokeista läpi ja niin edelleen.

Tehostetun kisällioppimisen menetelmää ruvettiin näiden ajatuksien pohjalta kehittämään Helsingin yliopiston tietojenkäsittelytieteen laitoksella vuonna 2010 alkupään ohjelmointikursseja varten. Laitoksella oli havaittu, että oppilaat kyllä oppivat luentomuotoisessa opetuksessa vastaamaan oikein kurssikokeisiin, mutta luentotilanne ei varsinaisesti valmistanut heitä ohjelmoinnin osaamiseen. Koska ohjelmointia opitaan ohjelmoimalla, ruvettiin opetusjärjestelyitä siirtämään pois luentosaleista ja painopiste opetuksessa siirrettiin opiskelijoiden itsenäisen työskentelyn tukemiseen.

Luonnollisesti tämä vaati opetusjärjestelyiden, materiaalin ja sisältöjen täydellistä uudistamista. Tapa, jolla laskuharjoitusassistentteja käytetään osana kursseja, täytyi miettiä täysin uusiksi. Koska opiskelijoiden tekemät tehtävät nousivat niin keskeiseen asemaan, täytyi ne uudistaa ja sisältöjen jaksotusta sekä tarkoituksenmukaisuutta jouduttiin kehittämään.

Ohjelmoinnin opetuksesta saatujen hyvien kokemuksien siivittämänä samanlaista ajattelumallia päädyttiin kokeilemaan Helsingin yliopiston matematiikan opetuksessa keväällä 2011. Luonnollisesti oppimistilanteet matematiikassa ja ohjelmoinnissa eroavat toisistaan, mutta tehostetun kisällioppimisen menetelmän peruselementit pysyvät samoina. Peruselementtejä ovat asiantuntijuuteen kasvaminen henkilökohtaisen ponnistelun kautta ja sen tukeminen opetusjärjestelyin, jotka mahdollistavat jatkuvan kaksisuuntaisen palautteen. Matematiikan opetuksessa opetusjärjestelyitä ja tehtäviä piti siis muuttaa, varsinkin kun syksyllä 2011 menetelmä skaalattiin toimimaan suurilla yli 400 opiskelijan kursseilla. Kehitystyö jatkuu edelleen sekä tietojenkäsittelytieteessä että matematiikan opetuksen kehittämisessä, josta jälkimmäistä voi seurata Kumpula opettaa -blogin kautta.

Tehostetun kisällioppimisen menetelmää on kokeiltu myös lukion matematiikan opetuksessa hyvin tuloksin. Jälleen menetelmää on pitänyt muokata sopimaan lukion oppimistilanteeseen. Lukiokurssien materiaaleissa etenkin tehtäviä pitää uudistaa soveltuviksi opetusmenetelmälle. Kisallioppiminen.fi-sivulle luodaan vuosina 2015-2017 uusien lukion opetussuunnitelmien perusteiden mukaisia avoimia oppimateriaaleja matematiikan opiskeluun ja opettamiseen. Materiaalit on erityisesti suunniteltu tukemaan tehostetun kisällioppimisen menetelmän käyttöä. Työ tehdään Helsingin kaupungin Mäkelänrinteen lukion ja Helsingin yliopiston matematiikan ja tilastotieteen laitoksen välisenä yhteistyönä. Hanketta rahoittaa Teknologiateollisuuden 100-vuotissäätiö.

Keväällä 2016 periodissa 5 kokeillaan ensimmäistä kertaa näitä uusia materiaaleja kurssilla MAA5 Mäkelänrinteen lukiossa. Tämä kurssi muuttuu MAA4:ksi syksyllä uuden opetussuunnitelman perusteen myötä. Tässä blogissa seurataan tiivisti tämän kokeilun vaiheita.

Aiheesta lisää:

• Vikberg T., Oinonen L. & Rämö J. (2015): Tehostettu kisällioppiminen matematiikan yliopisto-opetuksessa. Yliopistopedagogiikka.
• Lahdenperä J. (2015): Opiskelijoiden matemaattinen osaaminen tehostetun kisällioppimisen menetelmässä. Pro gradu -työ. Helsingin yliopisto.
• Torkkeli M. (2015): Opiskelijoiden kokemukset matematiikan tehostetussa kisällioppimisessa lukiossa. Pro gradu -työ. Helsingin yliopisto.
• Rämö J., Oinonen L. & Vikberg T. (2015). Extreme Apprenticeship – Emphasising Conceptual Understanding in Undergraduate Mathematics. In K. Krainer & N. Vondrová (Eds.), Proceedings of the Ninth Congress of the European Society for Research in Mathematics Education (pp. 2242–2248). Prague: Charles University in Prague, Faculty of Education and ERME.