Bayesiläinen keskiarvoistaminen yleisesti

Bayesilaiseen mallivalintaan kuuluu käytännössä kaksi osaa: ”havainnot generoineen” uskottavuusfunktion sekä tämän funktion parametrien priorin määrittäminen. Ensin mainittuun kuuluu epävarmuutta siinä missä jälkimmäiseenkin. Klassisessa tilastotieteessä on tapana kritisoida priorivalinnan subjektiivista luonnetta antaen ymmärtää tämän valinnan olevan jossain määrin tutkijan omista epätieteellisistä mieltymyksistä riippuvaista. Kuitenkin myös uskottavuusfunktion valinta on tutkijan enemmän tai vähemmän perusteltu valinta siinä missä priorikin. Molemmat valinnat perustuvat (yhtä lailla) tutkijan henkilökohtaiseen ennakkokäsitykseen havainnot tuottaneesta (fysikaalisesta) mekanismista. Uskottavuusfunktion valinta onkin harvoin jos koskaan aukottomasti perusteltu, vaan myös siihen liittyy käytännössä aina huomionarvoista epävarmuutta.
Bayesilaisessa mallin keskiarvoistamisessa (bayesian model averaging BMA) voidaan huomioida mallivalinnan epävarmuus kokonaisuudessaan pitäen sisällään sekä uskottavuusfunktion että priorin tutkijan subjektiiviseen harkintaan perustuneen mallivalinnan pätevyyden. Bayesilainen keskiarvoistaminen perustuu mallikokonaisuuden johtamiselle keskiarvoistamalla malli yli osamalliensa painotten kunkin osamallin vaikutusvaltaa niille datan valossa päivitettyjen posterioritodennäköisyyksien suhteessa (bayesin teoreeman avulla). Posterioritodennäköisyydeltään suurempi malli saa enemmän, pienempi malli vähemmän painoarvoa mallikokonaisuutta johdettaessa.
Tällöin oletetaan (kokonaistodennäköisyyden kaavassa), että jokin esitetyistä malleista on tosi. Esimerkiksi, jos jompikumpi kahdesta mallista M1 tai M2 on tosi ja on havaittu aineisto d, tällöin mallin yksi posterioritodennäköisyys saadaan kaavasta: p(M=1|d)=[p(d|M=1)*p(M=1)]/[p(d|M=1)*p(M=1)+ p(d|M=2)*p(M=2)]. BMA painottaa esimerkiksi posterioriennustavaa jakaumaa johdettaessa kutakin mallia edellä laskettujen posteriorien suhteissa.
Kun bayesilainen päättely yhdistetään toimintaan valitsemalla se toimintamalli, joka tuottaa parhaimman odotusarvoisen hyödyn, keskiarvoistetuilla malleilla saadaan oletettavasti parempi päätöksiä aikaisesti kuin yksittäisillä mallikokonaisuuden osamalleilla. Tämän voisi pyrkiä hahmottamaan siten, että keskiarvoistaminen huomioi paitsi useaan malliin liittyvän epävarmuuden, myös niihin liittyvän informaation. Suuremmalla määrällä informaatiota voidaan oletettavasti tehdä perustellumpi päätöksiä.
Kuten informaatioteoriaan perustuvat mallivalinnan kriteeri DIC ja BIC, myös BMA huomioi mallien yksinkertaisuuden (parsimony) arvona sinänsä mallin dataan sopivuuden (goodness-of-fit) rinnalla. Jälleen – kuten informaatioteoreettiset mallivalinnan kriteerit – myöskään BMA ei kykene huomioimaan sitä, jos kaikki estimointiin käytetyt/vertaillut mallit ovat huonoja. Roskan keskiarvo on keskimääräinen roska.
Siksi mallivalinnan perusteltavuuteen tarvitaan ennustavia jakaumia, joiden avulla voidaan mallin toimivuutta vertailla aitoon kerättyyn aineistoon. Ei voida tyytyä olettamaan, että joku osamalleista on tosi ja että mallikokonaisuus siksi toimii. Tulee tarkastella, kuinka hyvin (keskiarvoistetun) mallin ennusteet vastaavat todellisuutta. Paras tilanne on, jos voidaan ennustaa tulevia todellisia havaintoja, kuten Vantaanjoen smoltteja arvioitaessa johtamalla seuraavan päivän havaintojen posterioriennustava jakauma. Ennusteiden ja havaintojen yhteensopivuuden tarkastelu voidaan suorittaa paitsi visuaalisella tarkastelulla, myös määrämittaistamalla arvio esimerkiksi laskemalla niin sanottuja ”bayesilaisia p:n arvoja” (bayesian p-values). Logiikka toimii analogisesti nollahypoteesin testauksen logiikan kanssa, ainoastaan, että nollahypoteesi koskee (keskiarvoistettua) mallivalintaa sisällöttömän nollahypoteesin sijaan. Voidaan siis arvioida todennäköisyys havaita havaitun kaltainen (tai harvinaisempi/oudompi) aineisto, jos (keskiarvoistettu) mallivalintamme olisi oikea. Jos posterioriennusteet ovat huonoja, on malli todennäköisesti huono.
Smolttien totaalia estimoitaessa on keskeisenä ongelmana ollut juuri mallivalinta liittyen smolttien lähtötodennäköisyyksien jakauman muodolle tarkasteluaikavälin päivien yli. Tällä mallivalinnalla on myös kohtalaisen paljon vaikutusta saatuihin totaaliestimaatteihin. Kuten aina, yhtäkään mallivalintaa ei voida tässäkään varmuudella pitää totena tai epätotena, vaan ne ovat kaikki enemmän tai vähemmän epävarmoja. Lisäksi keskiarvoistamisen toimivuuden kannalta hyvänä asiana voitaneen pitää sitä, että mallit huomioivat ikään kuin hieman erilaisia vaihtoehtoisia näkökantoja smolttien muuttokäyttäytymiseen. Näin ollen on oletettavaa, että BMA -menetelmää soveltamalla saadaan mallivalinnan epävarmuuden paremmin huomioiva ja oletettavasti luotettavampi estimaatti mereen Vantaanjoesta muuttavien smolttien kokonaismäärälle.

Malliparametrien vertailu BMA-menetelmällä

Osana päivän tehtävänantoa yritimme soveltaa oppimaamme Carling & Chib-menetelmää omaan malliimme. Muodostimme vertailevan mallin kolmesta vaihtoehtoisesta smolttien lähtemistodennäköisyyttä kuvaavasta p-jakaumastamme.

Jakaumat muotoiltiin seuraavasti:

#p for the linear distribution
p[i,1]<-1/60

#p for the normal distribution
pl[i] <- exp(- pow((i-myy_p)/sd_p,2)*0.5)
p[i,2] <- pl[i] / sum(pl[1:60])

#p for the log-normal distribution
pn[i] <- (1/i)*exp(- pow(log(i)-location, 2) / scale)
p[i,3] <- pn[i] / sum(pn[1:60])

# Number of leaving trouts at day i
n[i]~dbin(p[i,model],N)

Muodostettiin jakaumia vertaileva malli. Painot eri malleille annettiin omiin kokemuksiimme niiden toiminnasta perustuen. Log-normaali jakauma sai pienimmän painon, sillä sen toimivuus on ollut kyseenalaista.

#prior for the model BMA for p

model~dcat(z[1:3])
z[1]<-2/5 #weight for the uniform distribution
z[2]<-2/5 #weight for the normal distribution
z[3]<-1/5 #weight for the log-normal distribution
Z[1]<-equals(model, 1)
Z[2]<-equals(model, 2)
Z[3]<-equals(model, 3)

Lisättiin vielä alkuarvot ladattavaksi ketjuille ennen mallin ajoa.

#Inits: use different initial value for each chain
list(model=1)
list(model=2)
list(model=3)

Alkuarvojen antamisessa ennen ajoa oli pieni ongelma, joka poistui kuitenkin, kun ne generoitiin ensin ja ladattiin vasta sitten.

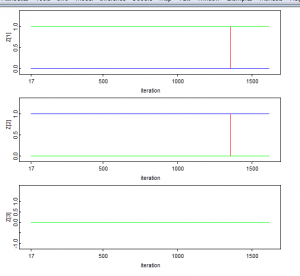
Ajon aikana todennäköisyyksien Z[1] ja Z[2] havaittiin selkeää ketjujen hyppimistä. Miksi Z[3] ei toiminut samoin?

Myös statistiikka Z[3]:n osalta näytti oudolta. Sen arvo oli tasan nolla.

Model-jakaumakin näytti sivuuttavan Z[3]:n kokonaan. Mistä tämä johtuu?

Opittavaa BMA:sta – teoria ja käytäntö

Tämän kappaleen alkuun on rehellisyyden nimissä todettava, että harva asia Bayeslaisen analyysin teoriassa tuskin tuntuu yhdellekään kurssilaiselle vielä täysin selkeältä. Bayesin kaavaan ja todennäköisyyksien päivittämiseen perustuva Bayeslaisen mallin perusajatus on toki suhteellisen suoraviivainen, mutta käytännössä on vaikeaa intuitiivisesti ymmärtää, miten esimerkiksi erilaiset priorivalinnat vaikuttavat posteriorijakaumiin. Lisäksi, koska käytännössä laskukaavoja ei koskaan voida soveltaa suoraan ja joudutaan turvautumaan laskennallisiin menetelmiin, tulee rakennetun mallin ymmärtämiseen mukaan uusi välivaihe – ohjelmisto, jolla itse laskenta suoritetaan, kuten projektissa käyttämämme BUGS.
Erilaisten mallin parametrien priorijakaumien vaikutus mallien posterioritodennäköisyyksiin BMA-analyysissa aiheutti ryhmässä pohdintaa. Lukemamme mukaan malleja vertailtaessa epäinformatiiviset priorijakaumat johtavat ’hyvin suuriin’ posterioritodennäköisyyksiin yksinkertaisten mallien tapauksessa. Miksi näin on? Millä perusteella eri mallien prioritodennäköisyydet täsmälleen päivittyvät?
Pohdimme myös erilaisten mallien prioritodennäköisyyksiä ja sitä, millä perusteella ne kannattaa määrittää. Kannattaako esimerkiksi aina käyttää tasaista prioria, vai kannattaako mieluummin käyttää omaa asiantuntija-arviota eri mallien sopivuudesta? Jos on jo havaittu tuloksia, voiko näitä huomioida arviossa vai pitääkö ne jättää huomioimatta?
Bayeslaisten p-arvojen käsite jäi myös toistaiseksi hieman hämäräksi.
Carlin & Chib – metodin käyttö BMA:n implikoinnissa BUGS – koodiin vaikutti mielestämme jokseenkin intuitiiviselta, mutta herätti silti useita kysymyksiä BUGSin muuttujiin ja funktioihin liittyvistä yksityiskohdista. Ymmärsimme, että eri mallien todennäköisyyksien päivittyminen varmasti tapahtuu samalla tapaa, kuin mallin muidenkin prioritodennäköisyyksien päivittyminen, mutta silti tähän liittyvä uusi syntaksi aiheutti pohdintaa siitä, miksi ja mitä kautta päivittyminen oikeastaan tapahtuu.
model –muuttujan määrittely tuntui esimerkkikoodeissa epäintuitiiviselta ja tuntui tapahtuvan hieman salaa allaolevan rakenteen mukaisesti
x ~ dnorm(mu[model],tau)
mu[1] < – a
mu[2] <- b

Tulkintamme mukaan ylläoleva määrittele model nimisen (1,2) vektorin.

Tämän lisäksi pohdimme BUGSin equals() –funktion toimintaa. Mitä täsmälleen tarkoittaa koodi P <- equals(model,1)

Luentokalvoilla myös sanotaan, että malli-indokaattoria ei yleensä tarvita sellaisille prioreille, jotka ovat malleille yhteisiä. Onko siis olemassa tilanteita, jossa tälle on kuitenkin tarve?