Tämä postaus on jatkoa muutamalle edelliselle postaukselleni, joissa käsittelin pyydystettävyyden mallintamista logistisella regressiomallilla. Ideana ja motivaationa tälle oli se, että käytetyn pyydyksen tehon epäiltiin riippuvan erityisesti veden korkeudesta.

Käsittelin logistista regressiomalli teoreettisesti ja kirjoitin hahmotelmaa siitä, miten malli voitaisiin määritellä BUGS-kielellä. Kuitenkin epäselväksi jäi se, miten prioritieto pyydystettävyydestä saataisiin mukaan malliin. Tämä postaus käsittelee tätä ongelmaa.

Logistinen regressiomalli on muotoa

logit(q) = a + beta[1]*VK +beta[2]*VL + E

VK=veden korkeus, VL=veden lämpötila, E=virhetermi , a= vakiotermi, beta[1] = veden korkeutta vastaava regressiokerroin, beta[2] = veden lämpötilaa vastaava regressiokerroin.

Haluaisimme siis ‘valita’ tämän mallin parametrit niin, että pyydystettävyyden priorijakauma olisi edelleen suurinpiirtein tietty beta-jakauma, kuten aiemminkin. Nyt, koska mallissa pyydystettävyys vaihtelee päivittäin, tarkoittaa tämä oikeastaan sitä, että arvioituna kaikkien päivien yli (tai oikeammin, arvioituna mallin selittäjien jakauman yli), noudattaisi pyydystettävyys haluttua beta-jakaumaa.

Aivan täsmälleen tätä haluttua tulosta emme voi saavuttaa, mutta niin sanotun informatiivisen g-priorin avulla pääsemme hyvin lähelle.

Ratkaistessa todennäköisyys logit-muunnoksesta, saadaan yhtälö

q = exp(x’B) / (1 + exp(x’B) )

jossa X on mallin selittäjät sisältävä matriisi (1, VK, VL) ja B näitä vastaavat kertoimet (a, beta[1], beta[2]).

On näytetty, että jos

B ~ N(b*e, g*n*(X’X)^-1)

ja

x ~ N(u, Z)

missä

b = digamma(a) – digamma(b)
g = [trigamma(a) + trigamma(b)] / p
e = c(1,0,..0) <- p-pituinen vektori
p = parametrien lukumäärä
n = havaintojen lukumäärä

N() = normaalijakauma

x = selittävät muuttujat

niin silloin

exp(x’B) / (1 + exp(x’B) )

vastaa suunnilleen beta-jakaumaa parametrein a ja b.

Tämä siis tarkoittaa, että on mahdollista rakentaa logistinen regressiomalli, jonka priorijakauma vastaa haluttua beta-jakaumaa.

Tämän voi todeta esimerkiksi R-ohjelmiston avulla seuraavasti. Alla olevassa koodissa X on niin kutsuttu design-matrix määriteltynä R-objektina (eli esim matriisi tai data frame, jonka ensimmäinen kolumni on 1, ja toinen ja kolmas esimerkiksi päivittäiset veden korkeudet ja lämpötilat). Koodin ajamiseksi tämä matriisi tulee siis ensin määritellä.

library(MASS)

X <- …

get.bg <- function(alpha, beta, parameters = 3) {
b <- digamma(alpha) – digamma(beta)
g <- trigamma(alpha) + trigamma(beta)
g <- g/parameters

return(c(b = b, g = g))
}

bg <- get.bg(alpha = 3, beta = 50)
Sigma <- bg[[‘g’]]*nrow(X)*solve(t(X) %*% X)
mu <- c(1,0,0)*bg[[‘b’]]

# B noudattaa multinormaalijaumaa, tässä otetaan siitä satunnaisotos
B <- mvrnorm(1000, mu = mu, Sigma = Sigma)

#  vektori, jossa todennäköisyyksiä logit-muunnoksesta
p <- apply(B,1,function(bi) {
apply(X,1,function(xi) {
exp(xi%*%bi)/(1+exp(xi%*%bi))
})
})
p <- c(p)

plot(density(p))

Kuvasta nähdään, että tuloksena on haluttu beta(a=3, b=50) jakauma

Tänään tuli puheeksi rysän uusi sijainti ja sen huomioiminen mallin sisällä. Rysä on aikaisemmin sijainnut joen haarautumiskohdassa ja on nyttemmin (13.5.) siirretty joen länsihaaran puolelle, hieman haarautumiskohdan yläpuolelle.

Saimme myös uutta mandariinikoetietoa, jonka mukaan nyt kaikkien kolmen kokeen aikana “vapautetusta” 188 mandariineista 139 on päätynyt joen länsihaaraan. Olemme käyttäneet tätä estimaattina smolttien vaeltamisesta, joten voisimme myös olettaa rysän pyytävän nyt tehokkaammin sen ollessa voimakkaimmin virtaavassa paikassa.

Hahmottelin helpohkon pikaratkaisun ongelmalle, jossa uutta rysää lähdetään yksinkertaisesti arvoimaan kokonaan uudella priorijakaumalla. Tämä ratkaisu ei edellyttäisi suuria muutoksia malliin:

Fyke_q[d]<-q_F*Fyke_op[d]*step(32-d)+q_F2*Screw_op[d]*step(d-32)

q_F2~dbeta(1,3)

Step-funktiot palauttavat yksinkertaisesti nollan erotuksen ollessa <0, jolloin summattava saa arvon nolla. Siis päivillä 1-32 käytetään rysän aiempaa priorijakaumaa q_F ja 32-60 uutta q_F2:ta. q_F2:lle annettu arvio hieman suuremmasta pyyntitehosta.

Tämä ratkaisu ei välttämättä ole ongelmaton. Rysän pyydystävyys päivittyy mielestäni datalla samaan tapaan kuin aikasemminkin. Se tarkoittaa, että kaikki rysän aikasemmassa paikassa sijaitessaan keräämä data pyydystettävyydestä siirtyy nyt “uudelle rysälle”, eli uudelle sijainnille. Tämä on mielestäni ristiriitaista sen kanssa, että rysän uuteen sijaintiin perustuva priori antaa nimenomaan ymmärtää, ettei sen pyydystävyys ole vain sen ominaisuus vaan riippuvainen myös sen sijannista. Tähän on syytä paneutua lisää ja katsoa miten tarkalleen riippuvuudet kulkevat pyydystävyys-mallin sisällä.

Pohdin aikaisemmin mallin kehittämisen näkökulmasta mahdollisuutta mallintaa erikseen joen länsi- ja itähaaraan päätyvien smolttien määrää. Tämä olisi hyödyllistä mikäli halutaan jatkossa selvittää esimerkiksi kuinka suuri osa smolteista joutuu länsihaaraan ja kuinka paljon voimalan läpi kulkeminen vaikuttaa niiden kuolleisuuteen. Olen nyt yrittänyt hieman hahmotella mitä tämänkaltainen mallinnus edellyttäisi. Ongelma ei sinänsä varmastikkaan olet teknisesti mitenkään hankala, mutta omalle hahmottamiselleni löytyy siitäkin runsaasti haastetta ja on siksi hyvää pohdintaa pelkästään oppimista ajatellen.

Tällä hetkellä vedessä on taas kaksi pyydystä, rysä ja smolttiruuvi. Ruuvi pyyntää joen itähaaraa, jossa siis kulkevat kalaportaat. Ruuvin sijainti on haarautumiskohdasta alavirtaan. Rysä on nyt siirretty pyytämään länsihaaraa, eli voimalan puolta, mutta se sijaitsee haarautumiskohdasta hieman ylävirtaan. Sijainnista johtuen ei voida olettaa varmasti, etteivät kalat voisi vielä rysän ohitettuaan siirtyä itähaaraan ja otaksuisin että voi olla jopa mahdollista smolttien ruuvin ohitettuaan palata vielä ylävirtaan ja mahdollisesti toiseen haaraan. Tämä varmasti lisää tuntematonta vaihtelua, mutta pohdintani oletuksena onkin nyt tilanne, jossa molemmat pyydykset sijaitsisivat selkeästi haarautumiskohdasta alavirtaan.

Millä tavalla tätä ongelmaa voitaisiin sitten mielestäni mallintaa?

Päivittäin vaeltavan smolttimäärän muutujan n[i]:n suhteen ei muutoksia tarvittaisi. Smoltteja saapuisi siis haarautumiskohtaan n[i]:n suuruinen määrä, jonka jälkeen ne valitsivat joko itäisen, tai läntisen haaran. Näille voisimme valita priorijakaumat tutkimuksen alussa tehdyn mandariinkokeen perusteella. Jakaumana käyttäsin tuttua beta-jakaumaa:

prob_w~dbeta(7,3)       #prioriodennäköisyys länsihaaran päätymiselle
prob_e~dbeta(3,7)       #prioritodennäköisyys itähaaraan päätymiselle

Nämä valitisin parametreiksi eri haaroihin päätyvien smolttien määrää kuvaavan binomijakaumaan:

nw[i]~dbin(prob_w, n[i])     #jakauma länsihaaraan matkaaville smolteille
ne <- n[i]-nw[i]                  #itähaaraan matkaavat smoltit

Saalis mallinnettaisiin molemmille haaroille erikseen binomijakaumana:

FykeX[i]~dbin(Fyke_q[i], nw[i])         #jakauma länsihaaraan saaliismäärälle
ScrewX[i]~dbin(Screw_q[i], nw[i])    #jakauma itähaaran saalismäärälle

Pyydystävyyden prioriarvoja pitäisi hiukan muuttaa. Rysälle prioritietoa mandariinikokeesta ei ole, ruuvin suhteen on huomiotava että nyt pyydystävyys mallintaisi vain itähaaran osuutta, ei smolttien kokonaismäärän pyydystävyyttä. Mandariinkokeen mukaan itähaaraan päätyi kaksi mandariinia, joista kaksi jäi pyydykseen:

q_S~dbeta (2,1)       #prioritodennäköisyys ruuvin pyydystävyydelle
q_F~dbeta (5,3)       #prioritodennäköisyys rysän pyydystävyydelle, mielivaltainen arvio

Näiden päivittäminen voisi tapahtua mielestäni samaan tapaan kuin ennenkin.

Priorien miettiminen on tässä tapauksessa suhteellisen helppoa. Itselleni alkoi tässä vaiheessa muodostua ongelmaksi juurikin ongelman laskennallinen ja looginen puoli. Itselleni on hankalaa hahmottaa jakaumien välillä tapahtuvia matemaattisia operaatiota ja yhdistää mallin osia loogisesti toisiinsa. Nyt minusta tuntuu, ettei malli näin päivitä ollenkaan eri haaroihin päätymismahdollisuuksien todennäköisyysjakaumia. Joudun vielä pohtimaan tarkemmin miten tämä tapahtuu. Myös kyseisten jakaumien suhteellisuus tulisi ottaa huomioon, kävisikö tämä vain jakamalla kukin molempien summalla? Näinkö saataisiin myös itähaaraan pyydystettävyys siirtymään posteriorijakaumiin?

Neuvot ovat tervetulleita!

Bayesiläinen keskiarvoistaminen yleisesti

Bayesilaiseen mallivalintaan kuuluu käytännössä kaksi osaa: ”havainnot generoineen” uskottavuusfunktion sekä tämän funktion parametrien priorin määrittäminen. Ensin mainittuun kuuluu epävarmuutta siinä missä jälkimmäiseenkin. Klassisessa tilastotieteessä on tapana kritisoida priorivalinnan subjektiivista luonnetta antaen ymmärtää tämän valinnan olevan jossain määrin tutkijan omista epätieteellisistä mieltymyksistä riippuvaista. Kuitenkin myös uskottavuusfunktion valinta on tutkijan enemmän tai vähemmän perusteltu valinta siinä missä priorikin. Molemmat valinnat perustuvat (yhtä lailla) tutkijan henkilökohtaiseen ennakkokäsitykseen havainnot tuottaneesta (fysikaalisesta) mekanismista. Uskottavuusfunktion valinta onkin harvoin jos koskaan aukottomasti perusteltu, vaan myös siihen liittyy käytännössä aina huomionarvoista epävarmuutta.
Bayesilaisessa mallin keskiarvoistamisessa (bayesian model averaging BMA) voidaan huomioida mallivalinnan epävarmuus kokonaisuudessaan pitäen sisällään sekä uskottavuusfunktion että priorin tutkijan subjektiiviseen harkintaan perustuneen mallivalinnan pätevyyden. Bayesilainen keskiarvoistaminen perustuu mallikokonaisuuden johtamiselle keskiarvoistamalla malli yli osamalliensa painotten kunkin osamallin vaikutusvaltaa niille datan valossa päivitettyjen posterioritodennäköisyyksien suhteessa (bayesin teoreeman avulla). Posterioritodennäköisyydeltään suurempi malli saa enemmän, pienempi malli vähemmän painoarvoa mallikokonaisuutta johdettaessa.
Tällöin oletetaan (kokonaistodennäköisyyden kaavassa), että jokin esitetyistä malleista on tosi. Esimerkiksi, jos jompikumpi kahdesta mallista M1 tai M2 on tosi ja on havaittu aineisto d, tällöin mallin yksi posterioritodennäköisyys saadaan kaavasta: p(M=1|d)=[p(d|M=1)*p(M=1)]/[p(d|M=1)*p(M=1)+ p(d|M=2)*p(M=2)]. BMA painottaa esimerkiksi posterioriennustavaa jakaumaa johdettaessa kutakin mallia edellä laskettujen posteriorien suhteissa.
Kun bayesilainen päättely yhdistetään toimintaan valitsemalla se toimintamalli, joka tuottaa parhaimman odotusarvoisen hyödyn, keskiarvoistetuilla malleilla saadaan oletettavasti parempi päätöksiä aikaisesti kuin yksittäisillä mallikokonaisuuden osamalleilla. Tämän voisi pyrkiä hahmottamaan siten, että keskiarvoistaminen huomioi paitsi useaan malliin liittyvän epävarmuuden, myös niihin liittyvän informaation. Suuremmalla määrällä informaatiota voidaan oletettavasti tehdä perustellumpi päätöksiä.
Kuten informaatioteoriaan perustuvat mallivalinnan kriteeri DIC ja BIC, myös BMA huomioi mallien yksinkertaisuuden (parsimony) arvona sinänsä mallin dataan sopivuuden (goodness-of-fit) rinnalla. Jälleen – kuten informaatioteoreettiset mallivalinnan kriteerit – myöskään BMA ei kykene huomioimaan sitä, jos kaikki estimointiin käytetyt/vertaillut mallit ovat huonoja. Roskan keskiarvo on keskimääräinen roska.
Siksi mallivalinnan perusteltavuuteen tarvitaan ennustavia jakaumia, joiden avulla voidaan mallin toimivuutta vertailla aitoon kerättyyn aineistoon. Ei voida tyytyä olettamaan, että joku osamalleista on tosi ja että mallikokonaisuus siksi toimii. Tulee tarkastella, kuinka hyvin (keskiarvoistetun) mallin ennusteet vastaavat todellisuutta. Paras tilanne on, jos voidaan ennustaa tulevia todellisia havaintoja, kuten Vantaanjoen smoltteja arvioitaessa johtamalla seuraavan päivän havaintojen posterioriennustava jakauma. Ennusteiden ja havaintojen yhteensopivuuden tarkastelu voidaan suorittaa paitsi visuaalisella tarkastelulla, myös määrämittaistamalla arvio esimerkiksi laskemalla niin sanottuja ”bayesilaisia p:n arvoja” (bayesian p-values). Logiikka toimii analogisesti nollahypoteesin testauksen logiikan kanssa, ainoastaan, että nollahypoteesi koskee (keskiarvoistettua) mallivalintaa sisällöttömän nollahypoteesin sijaan. Voidaan siis arvioida todennäköisyys havaita havaitun kaltainen (tai harvinaisempi/oudompi) aineisto, jos (keskiarvoistettu) mallivalintamme olisi oikea. Jos posterioriennusteet ovat huonoja, on malli todennäköisesti huono.
Smolttien totaalia estimoitaessa on keskeisenä ongelmana ollut juuri mallivalinta liittyen smolttien lähtötodennäköisyyksien jakauman muodolle tarkasteluaikavälin päivien yli. Tällä mallivalinnalla on myös kohtalaisen paljon vaikutusta saatuihin totaaliestimaatteihin. Kuten aina, yhtäkään mallivalintaa ei voida tässäkään varmuudella pitää totena tai epätotena, vaan ne ovat kaikki enemmän tai vähemmän epävarmoja. Lisäksi keskiarvoistamisen toimivuuden kannalta hyvänä asiana voitaneen pitää sitä, että mallit huomioivat ikään kuin hieman erilaisia vaihtoehtoisia näkökantoja smolttien muuttokäyttäytymiseen. Näin ollen on oletettavaa, että BMA -menetelmää soveltamalla saadaan mallivalinnan epävarmuuden paremmin huomioiva ja oletettavasti luotettavampi estimaatti mereen Vantaanjoesta muuttavien smolttien kokonaismäärälle.

Malliparametrien vertailu BMA-menetelmällä

Osana päivän tehtävänantoa yritimme soveltaa oppimaamme Carling & Chib-menetelmää omaan malliimme. Muodostimme vertailevan mallin kolmesta vaihtoehtoisesta smolttien lähtemistodennäköisyyttä kuvaavasta p-jakaumastamme.

Jakaumat muotoiltiin seuraavasti:

#p for the linear distribution
p[i,1]<-1/60

#p for the normal distribution
pl[i] <- exp(- pow((i-myy_p)/sd_p,2)*0.5)
p[i,2] <- pl[i] / sum(pl[1:60])

#p for the log-normal distribution
pn[i] <- (1/i)*exp(- pow(log(i)-location, 2) / scale)
p[i,3] <- pn[i] / sum(pn[1:60])

# Number of leaving trouts at day i
n[i]~dbin(p[i,model],N)

Muodostettiin jakaumia vertaileva malli. Painot eri malleille annettiin omiin kokemuksiimme niiden toiminnasta perustuen. Log-normaali jakauma sai pienimmän painon, sillä sen toimivuus on ollut kyseenalaista.

#prior for the model BMA for p

model~dcat(z[1:3])
z[1]<-2/5 #weight for the uniform distribution
z[2]<-2/5 #weight for the normal distribution
z[3]<-1/5 #weight for the log-normal distribution
Z[1]<-equals(model, 1)
Z[2]<-equals(model, 2)
Z[3]<-equals(model, 3)

Lisättiin vielä alkuarvot ladattavaksi ketjuille ennen mallin ajoa.

#Inits: use different initial value for each chain
list(model=1)
list(model=2)
list(model=3)

Alkuarvojen antamisessa ennen ajoa oli pieni ongelma, joka poistui kuitenkin, kun ne generoitiin ensin ja ladattiin vasta sitten.

Ajon aikana todennäköisyyksien Z[1] ja Z[2] havaittiin selkeää ketjujen hyppimistä. Miksi Z[3] ei toiminut samoin?

Myös statistiikka Z[3]:n osalta näytti oudolta. Sen arvo oli tasan nolla.

Model-jakaumakin näytti sivuuttavan Z[3]:n kokonaan. Mistä tämä johtuu?

Opittavaa BMA:sta – teoria ja käytäntö

Tämän kappaleen alkuun on rehellisyyden nimissä todettava, että harva asia Bayeslaisen analyysin teoriassa tuskin tuntuu yhdellekään kurssilaiselle vielä täysin selkeältä. Bayesin kaavaan ja todennäköisyyksien päivittämiseen perustuva Bayeslaisen mallin perusajatus on toki suhteellisen suoraviivainen, mutta käytännössä on vaikeaa intuitiivisesti ymmärtää, miten esimerkiksi erilaiset priorivalinnat vaikuttavat posteriorijakaumiin. Lisäksi, koska käytännössä laskukaavoja ei koskaan voida soveltaa suoraan ja joudutaan turvautumaan laskennallisiin menetelmiin, tulee rakennetun mallin ymmärtämiseen mukaan uusi välivaihe – ohjelmisto, jolla itse laskenta suoritetaan, kuten projektissa käyttämämme BUGS.
Erilaisten mallin parametrien priorijakaumien vaikutus mallien posterioritodennäköisyyksiin BMA-analyysissa aiheutti ryhmässä pohdintaa. Lukemamme mukaan malleja vertailtaessa epäinformatiiviset priorijakaumat johtavat ’hyvin suuriin’ posterioritodennäköisyyksiin yksinkertaisten mallien tapauksessa. Miksi näin on? Millä perusteella eri mallien prioritodennäköisyydet täsmälleen päivittyvät?
Pohdimme myös erilaisten mallien prioritodennäköisyyksiä ja sitä, millä perusteella ne kannattaa määrittää. Kannattaako esimerkiksi aina käyttää tasaista prioria, vai kannattaako mieluummin käyttää omaa asiantuntija-arviota eri mallien sopivuudesta? Jos on jo havaittu tuloksia, voiko näitä huomioida arviossa vai pitääkö ne jättää huomioimatta?
Bayeslaisten p-arvojen käsite jäi myös toistaiseksi hieman hämäräksi.
Carlin & Chib – metodin käyttö BMA:n implikoinnissa BUGS – koodiin vaikutti mielestämme jokseenkin intuitiiviselta, mutta herätti silti useita kysymyksiä BUGSin muuttujiin ja funktioihin liittyvistä yksityiskohdista. Ymmärsimme, että eri mallien todennäköisyyksien päivittyminen varmasti tapahtuu samalla tapaa, kuin mallin muidenkin prioritodennäköisyyksien päivittyminen, mutta silti tähän liittyvä uusi syntaksi aiheutti pohdintaa siitä, miksi ja mitä kautta päivittyminen oikeastaan tapahtuu.
model –muuttujan määrittely tuntui esimerkkikoodeissa epäintuitiiviselta ja tuntui tapahtuvan hieman salaa allaolevan rakenteen mukaisesti
x ~ dnorm(mu[model],tau)
mu[1] < – a
mu[2] <- b

Tulkintamme mukaan ylläoleva määrittele model nimisen (1,2) vektorin.

Tämän lisäksi pohdimme BUGSin equals() –funktion toimintaa. Mitä täsmälleen tarkoittaa koodi P <- equals(model,1)

Luentokalvoilla myös sanotaan, että malli-indokaattoria ei yleensä tarvita sellaisille prioreille, jotka ovat malleille yhteisiä. Onko siis olemassa tilanteita, jossa tälle on kuitenkin tarve?

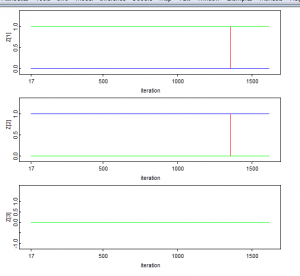
Muutoksia malliin: uusi pyydystystapa sekä priorioletusten päivittäminen

Pyydystystavan muutoksen huomioiminen mallissa

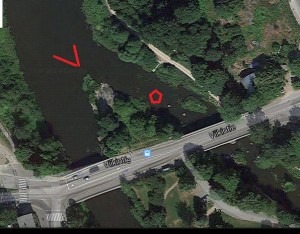
Päivän 16 kohdalla tapahtui tutkimusasetelman kannalta mielenkiintoinen muutos, kun datan lähteeksi joelle lisättiin Taimenruuvin lisäksi Taimenrysä, joka sijaitsee joen haaraumassa suunnilleen kuvan osoittamalla tavalla.

Kuva 1. Pyydysten sijainnit

Tämä tietysti vaikuttaa oleellisesti päivittäisen saalismäärän jakaumaan. Koko mallimme rakenne on karkeasti kuvattuna suunnilleen seuraavanlainen:

N & p -> n , n & q -> x

N = lähtevien taimenten kokonaismäärä

p = päivittäinen lähtötodennäköisyys

n = päivittäisten lähtijöiden lukumäärä

q = pyydystystodennäköisyys

x = pyydystettyjen taimenten lukumäärä

Eli kokonaislukumäärä ja päivittäinen lähtötodennäköisyys määräävät päivittäisten lähtijöiden lukumäärän jakauman, joka taas yhdessä pyydystystodennäköisyyden kanssa määrittää kiinnijääneiden lukumäärän jakaumaan. Tämä hierarkisen rakenteen ansiosta pyydykseen jääneiden kalojen lukumäärä päivittää esimerkiksi arviotamme kokonaislukumäärästä (N).

Taimenrysän tullessa peliin mukaan, täytyy pyydystystodennäköisyys määrittää uudestaan. Rysä ja ruuvi eivät vaikuta toistensa toimintaan, mutta sama kala ei voi jäädä kiinni molempiin. Siis:

P(kala jää ruuviin TAI rysään) = P(kala jää rysään) + P(kala jää ruuviin) – P(kala jää ruuviin JA rysään)

BUGS-koodilla tämä näyttää seuraavalta. (En käy läpi koodin yksityiskohtia; jos BUGS ei sinua kiinnnosta, siirry alas muuttointensiteettiä käsittelevään kappaleeseen!)

# Total cathability

q <- q_f + q_s – q_f * q_s

#separate catchabilities for both catching methods

# a=number of recaptures

# b=number of marked smolts not recaptured on the next day

# q_s=catchability of the smolt screw

q_s~dbeta(alpha,beta)

alpha<-(2 + sum(a[1:m[2]]))

beta<-(8 + sum(b[1:m[2]]))

# q_f=catchability of the fyke, that has been operational from day 15

q_f~dbeta(alpha2,beta2)

alpha2<-(2+(sum(a2[15:m[2]])))

beta2<-(8+(sum(b[15:m[2]])))

Nyt kun pyyntitodennäköisyys on uudelleenmääritelty, täytyy vielä mallissa huomioida, että muutos tapahtui tiettynä päivänä. Toteutimme tämän step-funktion avulla seuraavasti:

for(i in 1:m[1]) {

.

.

.

# catchability changed from day 16

lambda[i] <- q_s*n[i]*step(15-i) + q*n[i]*step(i-16)

# x[i] = the daily catch (num. of fish caught at day i)

x[i]~dpois(lambda[i])

}

Data näyttää mallissa nyt seuraavalta:

list(m=c(60,20))

x[]  a[]  a2[]      b[]

0    0    0    0

0    0    0    0

0    0    0    0

1     0    0    0

2     0    0    0

2     0    0    3

0    0    0    2

0    0    0    0

0    0    0    0

1     0    0    0

1     0    0    1

1     0    0    1

0    0    0    1

2     0    0    0

1     0    0    2

1     0    0    1

1     0    0    1

1     0    0    1

2     0    0    1

5     0    0    3

Muuttointensiteettiä koskevan priorioletuksen päivittäminen

Yhtenä oleellisena haasteena – sekä tarkkailuaikana kokonaisuudessaan Vantaanjoesta mereen siirtyvien smolttien totaalin posterioriestimoinnissa, että seuraavan päivän muuttomäärän estimoinnissa – on määrittää, kuinka muuttointensiteetti vaihtuu päivien kuluessa. Tämän suhteen asiantuntijatietoon perustuvana priorina käytettiin arviota, jonka mukaan a) muutto lähtee (luonnon olosuhteissa) toden teolla käyntiin noin 7 celsius -asteessa sekä b) muutto saavuttaa huippunsa 8 asteen tienoilla. Arvelimme intensiteetin huipun tämän perusteella saavutettavan siis jo seurannan alkuvaiheilla hahmotellen, että päivittäiset muuttomäärät laskevat huipun saavutettuaan hitaammin kuin olivat nousseet, hiipuen pikkuhiljaa lähtötasolle seurannan loppuessa noin 60 päivän jälkeen. Oletamme, että kaikki joessa majailevat smoltit lähtevät liikkeelle seuranta-ajan kuluessa. Tämä olettamus tuskin kirjaimellisesti pitää paikkansa, sillä jo ensimmäisinä päivinä saimme haaviin muutamia havaintoja, mikä antaa ymmärtää, että oletettavasti smoltteja on kulkenut vanhankaupunginkosken ohi jo ennen seurannan aloittamista.

Ennen kaikkea yllä tehdyn priorioletuksen b) perusteella päätimme arvioida yksittäisen smoltin todennäköisyyttä lähteä liikkeelle päivänä i vahvasti oikealle vinolla funktiolla. Tämän kaltaista jakaumamuotoa voitaisiin lähteä approksimoimaan esim. jonkinlaisella muunnelmalla Pareto-, Gamma- tai lognormaalijakaumasta. Päädyimme lognormaalin kaltaiseen funktioon, jonka varmistimme täyttävän todennäköisyysjakauman määritelmän määrittelyjoukossaan jakamalla funktion antamat arvot kaikkien arvojen summalla.

Havaitsimme kuitenkin pian, että lognormaalijakaumalla tullaan olettaneeksi aivan liian suuren osuuden smolteista lähteneen liikkeelle seurannan alkupäivinä. Tämän oletuksen seurauksena yksittäisten päivien muuttoestimaatit vaikuttivat liian korkeilta jo havaituille päiville. Samaisesta syystä totaaliestimaatti vaikutti arvioivan todellista muuttomäärää alakanttiin. Uumoilimme, että muuttohuippu ollaan vasta saavuttamassa ja joko että 1) kasvu huipulle tultaessa ei ole niin jyrkkään – ainakaan seurannan ensimmäisinä päivinä – kuin lognormaalijakauma olettaa, tai 2) että kasvu on vielä jyrkempää, mutta täysin äkillistä. Ehkäpä tiettyjen biologisten ennakkoehtojen kuten sopivan lämpötilan ja valonmäärän osuessa kohdalle, lukemattomat smoltit lähtevät liikkeelle samanaikaisesti.

Kuvio 1. Smolttien ennustetut odotusarvoiset muuttomäärät päivien funktiona mallivalinnalla lognormaali

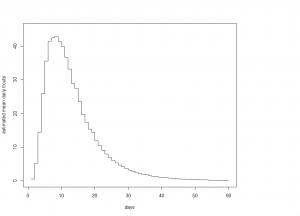
Kuten kuviosta 1 havaitsee, mallioletuksella lognormaali smolttien muuton huipun pitäisi jo olla takanapäin, sillä tänään 29.5. olemme päivässä nro 21. Tämä on ristiriidassa asiantuntijatiedon kanssa, jonka mukaan muuttaminen saavuttaa huippunsa noin kahdeksassa asteessa, mikä lämpötila saavutettiin eilen. Samaisesta syystä mallin estimoima suhteellinen muuttaneiden osuus kaikista joen smolteista vaikuttaa liian korkealta.

Korjausliikkeenä em. haasteeseen 1) päätimme muuttaa oletustamme muuttointensiteetistä. Lähdimme mallintamaan asiaa kahdella vaihtoehtoisella tavalla. Ensinnäkin datavetoisesti olettaen muuttotodennäköisyyden vakioksi yli päivien (ts P[i] = 1/60). Toiseksi olettaen jakauman normaaliseksi saavuttaen huippunsa odotusarvoisesti 25 päivän kohdalla. Saimme seuraavat estimaatit päiväkohtaisille muuttomäärien odotusarvoille:

Kuvio 2. Smolttien ennustetut odotusarvoiset muuttomäärät päivien funktiona mallivalinnalla tasajakauma ja normaalijakauma

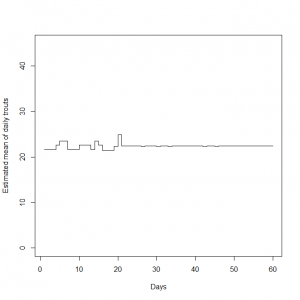
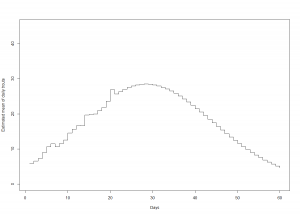
Nähdäksemme kyseisillä mallivalinnoilla on realistisemmat oletukset jo mereen muuttaneiden smolttien suhteellisesta osuudesta. Datavetoisella tasajakaumapriorilla saamme suhteessa havaittujen smolttien aineistossa esiintyneeseen tasaiseen trendiin perustellun oloisia estimaatteja. Normaalijakaumaoletuksella muuttohuippu on vasta edessä, minkä lisäksi pienempi osuus smolteista oletetaan jo muuttaneen kuin lognomaalioletuksella.

Edellä arveltiin, että menneiden tutkimusten perusteella saattaisi käydä niin, että muutto tapahtuu muutamassa harppauksessa sitten, kun se lähtee käyntiin. Näin ollen päivien yli oletetun muuttointensiteetin jakaumaan saattaa olla perusteltua tehdä yhä joitain kyseiset arviot paremmin huomioonottavia muokkauksia. Esimerkiksi voitaisiin olettaa, että muutto on tasaista (sitä kuvaa tasajakauma) tiettyyn päivään asti, jolloin jakauman muoto muuttuu ikään kuin kategorisena muuttointensiteetin tilan muutoksena. Tämä voidaan sisällyttää malliin olettamalla eri muuttoajanjaksoille (korkea / alhainen intensiteetti) omat niitä parhaiten kuvaavat todennäköisyysjakaumat esimerkiksi edellä jo esiintyneen step -funktion logiikkaa hyödyntäen.