Ruuvin pyydystettävyyden prioria mallinnamme binomijakauman konjugaatilla beta -jakaumalla. Valinta on kätevä laskettavuuden lisäksi sisällöllisesti siksi, että täten syntyvässä betabinomimallissa beta-(priori)jakauman parametrit voidaan ymmärtää niin sanottuina ”pseudohavaintoina”. Tämä tarkoittaa, että esimerkiksi alun perin käyttämämme priori Beta (2,8) muuntuu ajatusleikiksi, jossa olisimme saaneet kiinni ennen taimensmolttien muuttoon perustuvan ”varsinaisen” aineiston keruuta 2 kalaa (onnistumista) 10 kokeesta (eli 8 epäonnistumista).
Pseudohavaintopriorimme on perustunut mandariinikokeeseen, jossa on tarkasteltu, kuinka moni eri paikoista jokeen päästetyistä mandariineista on jäänyt ruuviin. Pseudohavaintojen painoarvoa olemme häivyttäneet suhteessa vapautettujen mandariinien todelliseen määrään siten, että lähes kahta sataa mandariinia koskeva aineisto on muunnettu 9 pseudohavainnoksi (1, 8). Tämä kielii mandariinien ja kalojen vertailtavuutta kohtaan tuntemastamme skeptisismistä.
Tämä skeptisyys on näkynyt pseudohavaintojen tarkkuudessa, ei oletuksena mandariinikokeen harhaisuudesta kalojen liikkeiden mallina. Olemme nimittäin määrittäneet pseudohavaintopriorimme siten, että onnistumisten (ruuviin jääneet kalat) ja epäonnistumisten suhde vastaa suoraan mandariinihavaintojen suhteita.
Pseudohavaintopriorimme sisältää siis piilo-oletuksen, jonka perusteella kalat ovat enemmän tai vähemmän kuin mandariinit. Eritoten oletamme, etteivät kalat kykene tietoisesti väistämään rysää tai ruuvia. Nimittäin jos kykenevät, tulisi yleistettäessä mandariinit kaloihin mandariinikokeen todellisten onnistumisten määrää pienentää suhteessa havaittuihin epäonnistumisten määrään.
Kuinka paljon priori sitten vaikuttaa tekemiimme päätelmiin?
Tarkastellaan asiaa kahdella heuristisella tavalla (tähänhän olisi käytössä mm. informaatioteoreettisia tarkkoja mittoja): vertailemalla ruuvin pyydystettävyyden posterioritodennäköisyyden moodia suurimman uskottavuuden estimaattiin sekä posterioritodennäköisyyteen, joka saataisiin, jos mallin rakentamiseen käytettäisiin informatiivisen sijaan maksimaalisen epäinformatiivista Jeffreysin prioria.
Suurimman uskottavuuden estimaatti määräytyy aineiston perusteella. SU -estimoinnissa selvitetään uskottavuusfunktion logiikan mukaisesti, millä parametrin arvolla havaittu aineisto olisi todennäköisin. Jos tässä ”aineisto” ymmärrettäisiin kalojen uudelleenpyyntidatana (jotta vertailu mandariineihin olisi mahdollisimman puhdas), olisi binomikokeen onnistumistodennäköisyyden suurimman uskottavuuden estimaatti yksinkertaisesti kiinniotettujen kalojen suhde kaikista merkatuista kaloista. Uusimmalla aineistolla tämä suhde on ruuvin kohdalla 2/72=1/36=0.0278.
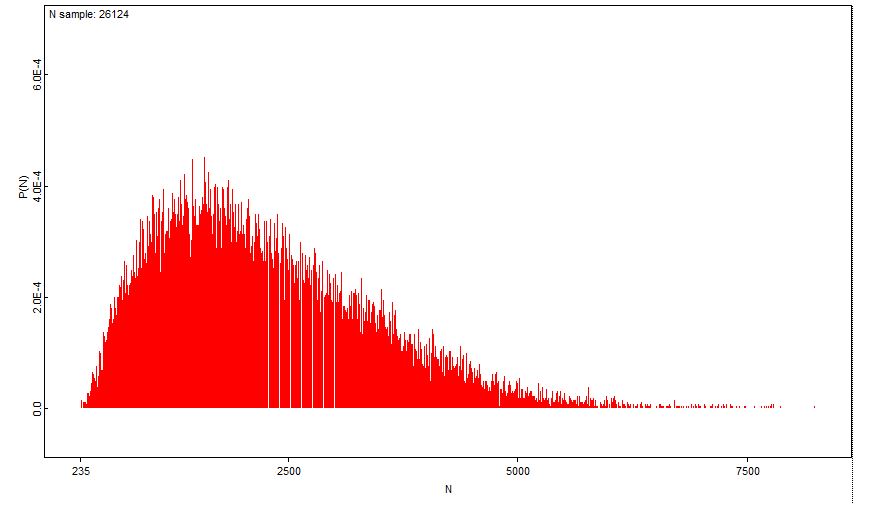
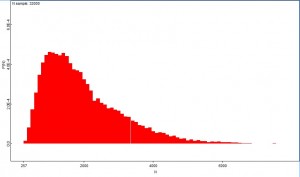
Tällä hetkellä ruuvin pyydystystehon posteriorimme näyttää seuraavalta:
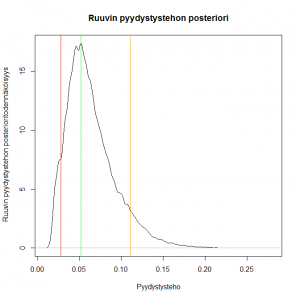
Kuvion punainen viiva näyttää suurimman uskottavuuden estimaatin, vihreä viiva posteriorimoodin ja oranssi priorimoodin paikan. Posteriorimoodimme on ymmärrettävästi suurimman uskottavuuden estimaattia korkeampi, onhan tätä myös priorimme (1/9). Posterioriestimaattimme asettuu SU -estimaatin ja priorimoodin väliin, jonkin verran lähemmäksi ensin kuin viimeksi mainittua.
Käytettäessä Jeffreysin epäinformatiivista prioria Beta (0.5;0.5) sekä ruuville että rysälle, saadaan ruuvin pyydystettävyydelle vain hieman vasemmalle varsinaisesta mallistamme siirtynyt posteriorijakauma.
Käyttämämme pyydystettävyysmallin posteriorin keskiarvo on 0.064 (noin 1/16) ja 95 % luottamusväli (0.022; 0.136). Pyydystettävyyden posteriorin keskiarvo Jeffreysin priorilla on puolestaan 0.055 ja 95 % luottamusväli (0.018; 0.129). Jeffreysin priori nostaa aineiston vaikutusvaltaa ja hilaa täten posterioria kohti suurimman uskottavuuden estimaattia (1/36) ja pois priorimoodista (1/9).
Onko mandariini siis kala? Vaikuttaisi siltä, että informatiivinen beta -priorimme on ”ristiriidassa” havaitun aineiston kanssa ja mandariini ei tämän perusteella vaikuttaisi olevan kala. Todennäköisyys havaita 2 tai vähemmän kalaa 72 kokeella, jos mandariinipseudohavaintomme 1/9 vastaisi todellista pyydystystehoa, on noin 1 % (nollahypoteesin testauksen hirviölogiikalla).
Huomionarvoista on, ettei ero pyydystettävyyden posteriorissa ole kuitenkaan kovin suuri, vaikka siirryttäisiinkin käyttämään epäinformatiivista Jeffreysin prioria (posteriorin keskiarvo siirtyy 1/16 -> 1/18).
Yksi tapa sisällyttää mandariinihavaintojen kalojen priorina käyttämiseen liittyvät epäilyksemme olisi rakentaa hierarkinen malli, jossa myös betapriorin parametrimme noudattaisivat omaa priorijakaumaansa. Tämä olisi oletettavasti perustellumpi ratkaisu haasteeseen kuin Jeffreysin priori. Onhan niin, että mandariinit välittävät jotain tietoa kalojen käyttäytymisestä, vaikka olisikin luonteeltaan harhaista ja epätarkkaa.