Category Archives: Kisällioppiminen

Kokemuksia uudesta arviointitavasta matematiikan yliopistokurssilla

|

”Tämä oli minulle normaalia matematiikan suorittamista huomattavasti motivoivampaa”

Kurssille Johdatus yliopistomatematiikkaan suunniteltiin keväällä 2018 kokonaan uusi arviointitapa. Kyseessä on matemaattisten tieteiden kandiohjelman ensimmäisen syksyn tai kevään 5 opintopisteen kurssi, jolla opitaan matemaattista ajattelua ja viestintää sekä perusasioita joukoista, kuvauksista ja muista tutkimusmatematiikan peruskäsitteistä. Kurssilla oli ollut käytössä väli- ja loppukoe, joihin sai lisäpisteitä laskuharjoituksista. Olimme uuden luennoitsijan, Mikko Stenlundin kanssa kuitenkin sitä mieltä, että tenttiarviointi ei oikein sovellu tälle kurssille. Tenttiarviointi nimittäin ohjaa opiskelijoita työskentelemään loppupainotteisesti ja pänttäämään ”tärppejä”, jotka helposti unohtuvat tentin jälkeen.

Kurssi on suurimmalle osalle opiskelijoita ensimmäinen matematiikan kurssi. Siksi halusimme alusta alkaen motivoida opiskelijat säännölliseen viikoittaiseen työskentelyyn. Toisaalta kurssilla opitaan asioita lähinnä tulevaa matematiikan opiskelua varten, joten emme halunneet, että opiskelijat opiskelevat asiat tenttiä varten ja unohtavat ne heti sen jälkeen. Lisäksi kurssille haluttiin lisätä itse- ja vertaisarviointia, koska nämä tukevat tutkimusten mukaan opiskelijoiden pystyvyyden kokemusta, hyviä opiskelustrategioita ja elinikäistä oppimista.

Kurssilla on hyvin heterogeeninen osallistujajoukko. Alla olevassa kaaviossa näkyy syksyn 2018 kurssin suorittaneiden jakauma eri koulutusohjelmiin. (Vanhoissa koulutusohjelmissa opiskelevat on kaaviossa pyritty yhdistämään vastaavaan uuteen koulutusohjelmaan.)

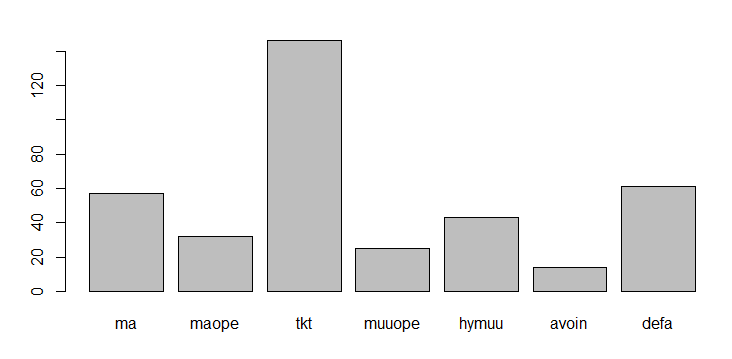
Kaavio suorittaneista eri koulutusohjelmissa

Syksyllä 2018 kurssin suorittaneiden jako eri koulutusohjelmiin (ma = matemaattisten tieteiden kandiohjelma, maope = matematiikan, fysiikan ja kemian opettajan kandiohjelma, tkt = tietojenkäsittelytieteen kandiohjelma, muuope = muu Helsingin yliopiston opettajaohjelma, hymuu = muu Helsingin yliopiston tutkinto-ohjelma, avoin = Avoimen yliopiston kautta suorittava, defa = Digital Education For All -hankkeen kautta suorittava)

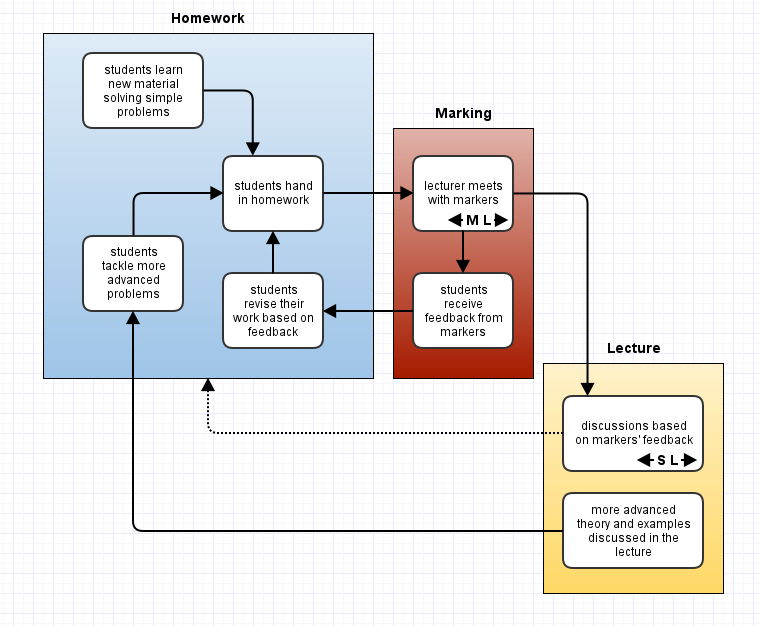
Suunnittelimme Mikon kanssa uuden arvioinnin, jossa ei ole lainkaan tenttiä, vaan arvosana perustuu suoraan erilaisista tehtävistä saataviin pisteisiin. (Arvioinnin toteuttamiseen osallistui myös kurssin toinen luennoitsija Timo Hänninen.) Kurssilla on käytössä Tehostetun kisällioppimisen menetelmä, jossa uusia asioita opiskellaan tehtävien avulla. Osa tehtävistä arvioidaan opettajien toimesta tai automaattisesti, ja osassa tehtäviä pisteitä saa pelkästä yrittämisestä.

Oheisessa taulukossa näkyy erilaisten tehtävien painotus arvosanassa. Viikkotehtävillä on hyvin suuri painoarvo. Suurin osa pisteistä tulee tehtävän laadun perusteella, mutta myös pelkällä tekemisellä on merkittävä rooli. Laadun perusteella arvioitavista tehtävistä saa palautetta joko opettajalta tai tietokoneelta, ja näitä saa palautteen jälkeen korjata ja palauttaa uudestaan.

Tehtävätyyppi suorituksen laatu
 yrittäminen
Viikoittaiset harjoitustehtävät 45 % 25 %
Itsearviointiharjoitukset – 10 %
Kurssin lopun laaja tehtävä 15 % –
Puolenvälin laajan tehtävän vertaisarviointi 5 % –

Kokonaan uutta kurssilla oli projektityyppinen lopputyö, joka nimettiin ”laajaksi harjoitustehtäväksi” kurssilla Algebra II tehtävän vastaavan työn mukaan. Lopputyössä opiskelijoille annetaan osaksi tai kokonaan uusi matemaattinen käsite, johon heidän on tutustuttava. Työssä opiskelijoita pyydetään muun muassa laatimaan uudelle käsitteelle matemaattinen määritelmä sekä lukemaan ja kirjoittamaan yksinkertaisia todistuksia käsitteeseen liittyen. Käsitettä on tyypillisesti myös kuvailtava omin sanoin ja piirroksin. Lopputyötä harjoitellaan kurssin puolessa välissä. Lopputyöstä saa ennen lopullista palautusta vertaispalautetta toisilta kurssilaisilta, ja lopullisen version tarkistavat ja pisteyttävät kurssin opettajat.

Syksyllä 2018 kerätyssä kurssipalautteessa kysyttiin uuteen arviointimenetelmään liittyviä kysymyksiä. Oheisesta taulukosta ja kaaviosta näkyy opiskelijoiden vastausten jakauma Likert 1–7 -asteikkoisiin kysymyksiin (1 = olen täysin eri mieltä, 7 = olen täysin samaa mieltä; n = 286). Erityisesti olimme iloisia, että opiskelijat kokivat vahvasti voivansa hyödyntää oppimaansa tulevilla kursseilla ja että he haluaisivat osallistua samalla tavalla suoritettavalle kurssille uudestaan.

Kysymys keskiarvo keskihajonta
Pystyin näyttämään osaamiseni kurssilla ja sain siitä tunnustusta 4,92 1,45
Koen voivani hyödyntää oppimiani asioita tulevilla kursseilla 5,69 1,37
Haluaisin osallistua tällä tavalla suoritettavalle kurssille uudestaan 5,73 1,50
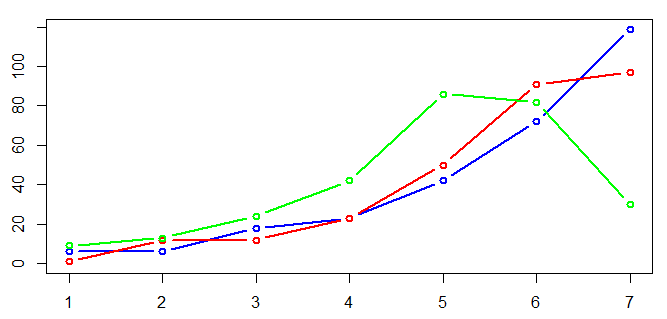
Likert-vastauksia kurssilla JYM, syksy 2018

Vastausten lukumääriä Likert-asteikkoisiin palautekysymyksiin (vihreä = ”Pystyin näyttämään osaamiseni ja sain siitä tunnustusta”, punainen = ”Koen voivani hyödyntää oppimiani asioita muilla kursseilla”, sininen = ”Haluaisin osallistua tällä tavalla suoritettavalle kurssille uudestaan”)

Numeeristen vastausten lisäksi opiskelijat vastasivat avoimeen kysymykseen ”Mitä mieltä olet kurssin suoritusmenetelmästä?” Vastaukset olivat lähes poikkeuksetta positiivisia: 286 vastauksen joukossa oli vain seitsemän kriittistä vastausta (2,4%).

Vastauksia analysoitiin aineistolähtöisellä laadullisella sisällönanalyysillä, jotta saataisiin selville, mitä hyötyä opiskelijat kokevat saavansa uudesta arviointimenetelmästä. Vastaukset voitiin ryhmitellä kolmeen kategoriaan.

  1. Suurimmassa kategoriassa opiskelijat korostivat, että arviointimenetelmä motivoi työskentelemään jatkuvasti koko kurssin ajan. He sanoivat tällaisen jatkuvan työskentelyn tukevan heidän oppimistaan, ja lisäksi tukevan hyvää työskentelyrutiinia.
  2. Toiseksi suurimmassa kategoriassa kehuttiin kurssin kokeettomuutta. Vastaajien mukaan se vähentää stressiä ja kannustaa keskittymään pänttäämisen sijaan asioiden opiskeluun ja omaan oppimiseen.
  3. Kolmannessa kategoriassa viitattiin siihen, että pisteiden jatkuva kertyminen antaa paremman kuvan osaamisesta kuin yksittäinen tentti.

Ohessa joitakin kuvaavia sitaatteja opiskelijoiden vastauksista.

”Pidin siitä, että kurssi kannusti tekemään tehtäviä jatkuvasti, jolloin oppiminen oli palkitsevampaa ja paremmin mieleen jäävää, kuin jos esimerkiksi kurssi suoritettaisiin yhdellä tai useammalla kurssikokeella, joihin pitäisi valmistautua erikseen.”

”Tehtäviin eikä tenttiin painottava arviointi kannustaa opiskelemaan itseä, ei tenttiä varten.”

”Tämä oli minulle normaalia matematiikan suorittamista huomattavasti motivoivampaa. Aikasemmat kokemukseni ovat lukio- ja amk-matikasta, missä oksennetaan useiden kuukausien työ yhdelle tenttipaperille […] Aiemmin on ollut hirveä kammo tätä oppiainetta kohtaan, ja lähdinkin mukaan haastamaan itseäni. Yllätys oli iso kun tajusin, että konkreettisesti kaikki työ mitä jaksan tehtäviin laittaa, näkyy kurssin loppuarviossa.”

Joissakin palautteissa esiintyi kuitenkin myös kritiikkiä kokeettomuutta kohtaan:

”Minusta tässä uudessa systeemissä että loppukoetta ei ole ja kurssinumero tulee vain sen perusteella miten hyvin suoriutuu laskuharjoituksista […] on se ongelma että tässä arvosana kertoo sen miten hyvin asian on osannut silloin kun sitä on vasta opetellut, eikä sitä miten hyvin asian osaa kurssin jälkeen […] Tämän takia loppukoe antaisi minusta paremman arvion siitä miten hyvin opiskelija osaa kurssin asiat.”

Yleisesti ottaen opiskelijapalautteessa esiintyi sekä kehuja että kritiikkiä, joka otetaankin huomioon seuraavissa toteutuksissa. Esimerkiksi tehtäviä koettiin olevan liian paljon opintopistemäärään nähden, ja osa opiskelijoista koki laajat harjoitustehtävät ahdistaviksi, koska ne olivat niin avoimia ja soveltavia. Tehtävämäärää pyritään jatkossa vähentämään, ja laajoja harjoitustehtäviä ohjeistamaan paremmin, jotta ne eivät säikäytä opiskelijoita.

Positiivisena huomiona on lopuksi todettava, että palautteen mukaan kurssi on lisännyt monien opiskelijoiden kiinnostusta matematiikkaa kohtaan. Osa opiskelijoista on sanonut haluavansa kurssin myötä ottaa lisää matematiikan kursseja tai ottavansa matematiikan sivu- tai jopa pääaineeksi. Kaiken kaikkiaan kurssia ja sen suoritusmenetelmää on pidettävä onnistuneena, ja sen kehittämiseen edelleen kannattaa panostaa!

”Kiitoksia erinomaisesta kurssista! Kurssi herätti itselläni syvällisemmän mielenkiinnon matematiikkaa kohtaan, jossa aiemmin en ole kokenut olevani erityisen hyvä. Tämä toimi mielestäni hyvänä esimerkkinä miksi valita Helsingin Yliopisto kaikista vaihtoehdoista. Toivottavasti vastaavia kurssimuotoja on saatavilla aineopinnoissakin!”

Tässä kirjoituksessa esitetyt uutta arviointimenetelmää koskevat tulokset esiteltiin ensimmäistä kertaa Pedaforum 2019 -konferenssissa Kumpulan kampuksella 6.6.2019.

Tehostettu kisällioppiminen

|

Kirjoittajat: Johanna Rämö, Jokke Häsä

Kisällioppimisessa pääosassa on opiskelijoiden työskentely, johon he saavat henkilökohtaista ohjausta. Opiskelijat oppivat taitoja, joita tarvitaan myöhemmillä kursseilla ja työelämässä. Matematiikan opiskelijat pääsevät työskentelemään heti alusta alkaen samaan tapaan kuin matemaatikot: ratkomaan ongelmia, keskustelemaan niistä toisten kanssa, etsimään tietoa ja kirjoittamaan todistuksia hyvän matemaattisen käytännön mukaisesti. Tällä tavalla he pääsevät välittömästi matemaatikkoyhteisön jäseniksi. Opetus koostuu harjoitustehtävistä, ohjauksesta sekä luennoista.

Uuden asian opiskelu alkaa tekemällä laskuharjoitustehtäviä yhdessä toisten opiskelijoiden kanssa. Tehtävien ratkaisemiseksi opiskelijoiden täytyy tutustua kurssimateriaaliin ja harjoitella siten matematiikan lukemista. Tehtävien ratkaisemisessa ja materiaalin lukemisessa auttavat ohjaajat, jotka päivystävät osaston oppimisympäristössä joka päivä.

Opiskelijat ja ohjaajat työskentelevät varta vasten suunnitellussa oppimisympäristössä, joka sijaitsee matematiikan ja tilastotieteen osaston pääkäytävällä. Ohjaajilla on päällään kirkasväriset liivit, jotta opiskelijoilla olisi matala kynnys ryhtyä keskustelemaan ohjaajan kanssa.

Ohjaajen tehtävänä on johdattaa opiskelija kohti ahaa-elämystä. He keskustelevat opiskelijan kanssa ja antavat hänen selittää omia ajatuksiaan. Näin opiskelijan kommunikaatiotaidot kehittyvät. Toisaalta ohjaajat auttavat opiskelijaa kartuttamaan opiskelutaitojaan kuten vaikkapa matematiikan lukemista ja tiedon etsimistä materiaaleista. Ohjaajat ovat vanhempia matematiikan opiskelijoita ja he saavat tukea työhönsä viikoittaisissa pedagogisissa tapaamisissa.

Työskentelyn jälkeen opiskelijat palauttavat viikoittaiset harjoitustehtävät kirjallisesti. Ohjaajat tarkistavat osan tehtävistä ja antavat niistä palautetta. Opiskelijoilla on sen jälkeen mahdollisuus korjata ratkaisujaan palautteen perusteella. Tällä tavoin opiskelijat saavat jatkuvaa palautetta osaamisestaan, ja he pääsevät harjoittelemaan matemaattisten todistusten kirjoittamista vähitellen. Kurssin opettajat puolestaan saavat tietää, mitä opiskelijat osaavat, ja voivat reagoida siihen opetuksessa.

Lopuksi, kun uusiin aiheisiin on tutustuttu tehtävien avulla, niitä käsitellään luennolla. Tehtäviä tekemällä opiskelijat ovat perehtyneet luentojen aiheisiin etukäteen, joten luennot voidaan käyttää asiayhteyksien valottamiseeen ja epäselviksi jääneiden asioiden käsittelyyn. Luennoilla voidaan keskittyä sellaisiin asioihin, jotka eivät välttämättä avaudu kurssimateriaalia lukemalla. Luennoitsija mallintaa esimerkkien avulla matemaatikon ajattelutapaa.

Luennoilla harjoitellaan myös matemaattista kommunikointia. Opiskelijoilla on aktiivinen rooli luennon etenemisessä ja he pääsevät keskustelemaan luennon aihepiireistä vierustoverinsa kanssa. Luennoitsija ohjaa keskustelua ja pitää huolen, että ilmapiiri on turvallinen ja salliva.

Luennon jälkeen opiskelijoilla on syventynyt käsitys opeteltavasta asiasta, ja he saavat seuraavalle viikolle haastavampia tehtäviä. Samalla aloitetaan myös uusiin aiheisiin tutustuminen valmistelevien tehtävien avulla. Näin oppimissykli toistuu viikosta toiseen.

Tutkimusten mukaan tehostetun kisällioppimisen menetelmä tukee opiskelijoiden oppimista ja lisää heidän aktiivisuuttaan (Rämö et al., 2015). Kisällioppimisella on myös myönteinen vaikutus opiskelijoiden opiskelustrategioihin ja matemaattisen pystyvyyden kokemukseen (Lahdenperä et al., 2018).

Kirjoitus on julkaistu alun perin Matematiikan opetuksen tutkimusryhmän sivuilla.
Kuvat: Veikko Somerpuro ja Susanna Oksanen

Lue lisää:

Lahdenperä, J., Postareff, L., & Rämö, J. (2018). Supporting quality of learning in university mathematics: a comparison of two instructional designs. International Journal of Research in Undergraduate Mathematics Education, 1–22.

Rämö, J., Oinonen., L., & Vikberg, T. (2015). Extreme Apprenticeship – Emphasising Conceptual Understanding in Undergraduate Mathematics. In K. Krainer, & N. Vondrová (Eds.), Proceedings of the Ninth Congress of the European Society for Research in Mathematics Education (pp. 2242–2248).

Vikberg, T., Oinonen, L. & Rämö, J. (2015). Tehostettu kisällioppiminen matematiikan yliopisto-opetuksessa. Yliopistopedagogiikka, 22(1), 36-39.

Kuinka maisterivaiheen kurssista muodostui matemaatikkojen yhteisö

|

Olen jo usean vuoden ajan käyttänyt kursseillani uutta opiskelijakeskeistä menetelmää, tehostettua kisällioppimista. Viime aikoinan olen opettanut vain suuria 1. ja 2. vuoden massakursseja, mutta viime keväänä pääsin opettamaan pientä maisteritason kurssia. Sovelsin kurssin opetuksessa tehostetun kisällioppimisen menetelmästä tuttuja elementtejä sekä Peter Liljedahlilta saatuja ideoita Ajattelevasta luokkahuoneesta (Thinking classroom).

Vaikka kokeilin kurssitoteutusta ensimmäistä kertaa, se toimi hämmästyttävän hyvin. Kun opiskelijat oppivat tuntemaan toisensa, syntyi kurssille poikkeuksellinen ilmapiiri. Monesti jäin vain ihmeissäni seuraamaan, kun opiskelijat keskustelivat keskenään kuulostaen ihka oikeilta matemaatikoilta. He yrittivät yhdessä ratkoa ongelmia tuoden keskusteluun omat ideansa ja synnyttäen siten lisää ideoita muissa. Tänä keväänä toteutin kurssin uudelleen tehden opetusmenetelmään pieniä korjauksia.

Opiskelijat harjoittelivat koko kurssin ajan ryhmätyötaitoja tekemällä tehtäviä yhdessä. Kuvassa rakennettavien Platonin kappaleiden symmetriat olivat yksi kurssin suosikkiaiheista toiminnallisuutensa vuoksi.

Kurssin opetus koostui

  • viikkotehtävistä
  • kurssimateriaalista, jota opiskelijat lukivat itsenäisesti
  • tehtävien tekoon ja materiaalin lukemiseen annetusta ohjauksesta
  • ryhmätyöskentelystä
  • oppimistesteistä, joilla opiskelijat arvioivat omaa osaamistaan ja jotka antoivat ohjeita opiskeluun
  • kahdenkeskisestä arviointikeskusteluista opettajan kanssa kurssin puolivälissä ja lopussa.

Kurssialustana toimi Moodle, jonne opiskelijat saattoivat laittaa ratkaisujaan toisten näkyville.

Kunakin viikkona oli kolme kahden tunnin tapaamista. Pääasiassa opiskelijat tekivät tapaamisissa tehtäviä omaa tahtiaan kurssimateriaalin avulla. Ohjasin heitä työskentelemään ryhmissä sen mukaan, mitä tehtävää kukin teki, ja kiertelin keskustelemassa tehtävistä ryhmien kanssa.

Käytin paljon aikaa siihen, että opiskelijat oppisivat tuntemaan toisensa ja heistä olisi luontevaa keskustella yhdessä matematiikasta. Tässä auttoi erityisesti ohjattu ryhmätyöskentely, jossa kaikki opiskelijat työskentelivät 2–3 hengen ryhmissä saman ongelman kimpussa. Yleensä otin ongelmat viikkotehtävien joukosta. Opiskelijat luonnostelivat ajatuksiaan liitutauluille, jolloin lopuksi oli helppo keskustella yhdessä heidän ratkaisuistaan. Tätä varten käytössä oli luokkahuone, jonka seinät olivat täynnä liitutauluja.

Opiskelijat pohtivat tehtäviä yhdessä ja kirjoittivat ajatuksensa taululle. Tällä tavoin niistä oli niistä helppo keskustella yhdessä koko ryhmän kesken.

Kurssilla ei ollut luentoja. Toisinaan saatoin kuitenkin pitää muutaman minuutin yhteisen puheenvuoron kooten vaikkapa yhteen jokin asiakokonaisuuden tai kertoen käsitteiden historiasta.

Joka viikko opiskelijat jaettiin pareiksi, jotka laativat ratkaisuehdotukseen yhteen viikkotehtävään. He kirjoittivat ratkaisun puhtaaksi yhdessä ja esittivät sen sitten muille. Näin harjoiteltiin sekä matematiikan kirjoittamista että siitä puhumista. Parit vaihtuivat viikoittain, jotta opiskelijat saivat työskennellä mahdollisimman monen eri ihmisen kanssa. Arvoin parit opiskelijoiden nähden samoin kuin heille jaettavat tehtävät. (Esimerkiksi korttipakka sopii tähän hyvin. Pakasta voi valita sopivan määrän kortteja ja ne, jotka saavat saman numeron, muodostavat parin.)

Ratkaisuehdotusten tekeminen voi olla opiskelijoille työlästä. Siksi valitsin tähän tarkoitukseen tehtävien joukosta melko helppoja tehtäviä. Jotta työmäärä pysyisi järkevänä, annoin kullekin opiskelijalle ratkaisuntekovuoroja vain joka toiselle viikolle. Muina viikkoina opiskelijat laativat parin virkkeen tiivistelmän jonkin tehtävän ratkaisusta. Näin ote kurssista ei herpaanunut, ja samalla opiskelijat saivat harjoitella ilmaisemaan matemaattisia ideoita ymmärrettävässä ja selkeässä muodossa.

Kurssilla oli viikkotehtävien lisäksi kaksi laajempaa harjoitustehtävää, jotka opiskelijat tekivät itsenäisesti ja joista annoin kirjallista palautetta. Opiskelijat saivat kehittää ratkaisujaan palautteen perusteella.

Kurssipalautteen perusteella opiskelijat pitivät uudesta opetusmuodosta. Suurin osa haluaisi osallistua vastaavalla menetelmällä opetetulle kurssille uudelleen. Tässä vielä joitakin poimintoja opiskelijapalautteesta:

”Mielestäni erittäin hyvä kurssi, toivon että laitokselle ilmestyisi enemmän vastaavanlaisia kursseja.”

”Kurssin muoto on todella mainio ja kannustava.”

”Tämä on loistava tapa opetella matemaattisen tekstin kirjoittamista ja ryhmätyöskentelyä, joten tämän tyylisiä kursseja on hyvä olla muutama tarjolla. Mielestäni näin olisi järkevää korvata pakollisia kieliopintoja.”

”Kiitos kurssista, se oli oikein hauska ja hyödyllinen kokemus, toivottavasti toimintamalli tulee käyttöön joissain muissakin kursseissa!”

Kurssilla ei ollut tenttiä, vaan arvosana määräytyi ohjatulla itsearvioinnilla. Tästä seuraa lisää tietoa myöhemmässä blogitekstissä.

Lue lisää:

Tuohilampi L., Rämö, J., Häsä, J., & Pekkarinen, E. (2017) Tiedonsiirrosta tiedon yhteiseen omistamiseen ja rakentamiseen – autonomian tukeminen Helsingin yliopiston matematiikan kurssikokeilussa. Toiveet ja todellisuus – kasvatus osallisuutta ja oppimista rakentamassa. Toom, A., Rautiainen, M. & Tähtinen, J. (toim.). Turku: FERA Suomen kasvatustieteellinen seura, s. 509-534 26 Sivumäärä (Kasvatusalan tutkimuksia; nro 75).

The Durham Experience, Part II

|

In the academic year 2014–2015 I had the privilege to teach a lecture course in Durham University in the United Kingdom. Durham is a rather prestigious university that is very selective in its student intake. In these entries I record some of my thoughts concerning the experience. Although I could only witness the system in Durham, many details can most likely be generalised to other UK universities.

(Read the previous post here.)

View of Durham

Lecturing Algebra II

Despite its name, Algebra II is the first course in abstract algebra offered in Durham. It is a second-year course, spanning the whole academic year. Compared to courses taught for example in Helsinki, the course covers roughly the material for a basic one-term algebra course plus a slightly shorter and more advanced course. The course had about 170 students.

I was eager to face the challenge of teaching a full-fledged lecture course in a new country. Having taught algebra before, I knew it to be a difficult topic that demands a lot of abstract thinking and becoming familiar with many new concepts. My colleagues in Durham had also warned me that it would be very difficult to get the students to appreciate how much and what kind of work they would have to do in order to learn the material effectively.

While I was planning my course, it soon became clear to me that to encourage the students to work in an effective manner for their own learning, I should implement methods that in the University of Helsinki go under the name “Extreme Apprenticeship Model”. This model has been applied to teaching certain mathematics undergraduate courses in the Department of Mathematics and Statistics since 2011. After its introduction, the model has enjoyed great success. In particular, it has been successful in engaging the students, teaching them good, professional-style studying habits, as well as making them more committed to their studies in the department.

It was, however, impossible for me to run a full-fledged Extreme Apprenticeship course since I had much less control over the teaching resources than is usual in Finland. Therefore I needed to adapt my teaching to a new environment. In such cases I find it useful to consider the motivations behind the practices in order to decide what is essential and what is not. Doing so, I found that I wanted to focus on

  1. Improving the students’ working habits.
  2. Enabling strong bi-directional feedback that would allow the students to know what is expected from them and the teaching to be guided by the students’ needs.
  3. Teaching abstract thinking and communicating these thoughts in speaking and writing.

Considering these points led me to implement roughly the following set of methods:

  • a form of flipped learning, in which the students would work individually for their own learning, and the lectures are used to solidify the students’ knowledge, build a general picture, weed out misconceptions, and discuss effective study methods
  • course notes designed for the students to be able to read and understand to a great extent by themselves
  • detailed descriptions of learning objectives and self-evaluation exercises based on them
  • weekly meetings with homework markers to ensure they would know what I require of the students, and that I would find out how the students are doing
  • the possibility of resubmitting certain homework questions in order to employ the markers’ comments if the first solution was not good enough
  • activating the students during the lectures with small group tasks, questions, and polling exercises
  • activating conceptual thinking through tasks that would require explaining, connecting and evaluating.

In short, the course ran in the following way. First, the students were given typed, well-prepared notes. They familiarised themselves with new concepts through simple homework problems. They would hand in the problems to be marked. Once the markers had had a few days to look at the scripts, we would meet together to discuss what the students had come up with. Then the markers would go back to finish the marking, while I would discuss the most common mistakes and important misconceptions in the lectures. I would use online voting systems in the lectures to help gauge the students’ learning pace and to promote meaningful discussions. The lectures would also progress to deeper theory and examples, and the next week’s homework would – in addition to preparatory material – also contain harder problems on topics that were discussed during the week.

Feedback flowchart of Algebra II

Running Algebra II. The arrows between boxes of different colour indicate the flow of information or feedback. The double arrows ML and SL symbolise bi-directional feedback between markers and lecturer and between students and lecturer.

There were two types of questions in the homework. Most of the questions were marked based on honest attempt whether the answer was right or wrong. For these questions, the markers were not required to comment anything if they did not have time for it. The students could later compare their solutions to the model solutions. On the other hand, a few questions were more substantial, usually requiring a written proof. These questions were marked based on the quality of the answer – not only of the mathematical correctness, but also the quality of writing. It the solution was not adequate in the first week, the student was encouraged to resubmit the question the following week and would receive the marks after the resubmission.

In applying the above methods, I faced several challenges. As already mentioned in my previous post, the lecture system in Durham is very rigid. My lecturing hours (twice 50 minutes a week plus a fortnightly “problems class”), as well as tutorials (50 minutes per a 15 person group fortnightly) were all prescribed to me. Also the teaching assistants giving the tutorials and marking the homework (mostly separate people, to my surprise) were decided for me. One major difference with Extreme Apprenticeship method in Helsinki was that I could not provide the students with a drop-in workshop with instructors that would always be present. Another challenge was that the other teachers in Durham that I got into contact with had very little experience about any of the methods I was going to apply, so I could not count on their advice as much as I was used to in Helsinki.

The biggest obstacle, however, was that the students were in general unaccustomed to anything else than the traditional teaching style where the lecturer writes on the blackboard and students take notes, which they then later refer back to when doing their homework. This limited background, of which I only learned gradually when I was already teaching the course, created a lot of mental opposition towards my teaching right from the start of the course. Of course, I was prepared to explain any new methods I would be using, so that the students would be aware of what was expected from them and how they would benefit from the diverse exercises, but in Durham I felt I was required to explain myself much more than usual. There was a constant need to reassure the students of the fact that they were indeed learning the necessary skills even when they did not recognise the “unconventional” methods we were using.

Despite initial misgivings, the students gradually learned to work in the new way, some quicker, some at a slower pace. However, student feedback questionnaires half-way through and at the end of the course show that the students were not in general happy with the lectures, saying that these were useless and not teaching them anything. Being inefficient is a well-known problem of mass lectures, and the amount of negative feedback on this aspect seems only to indicate that the students have not previously recognised this inefficiency. On the other hand, the prepared course notes received a lot of positive feedback. It seems to be very rare in Durham that the students would be given such complete sets of notes.

During the course, I observed the students closely in order to spot any learning difficulties resulting from the change in teaching style. Some individuals indeed claimed that they were facing serious difficulties, but on the whole I could see no significant indication that anything would be going wrong. Even if the students complained, they were still clearly learning. Their results in the final exam were as good as would be expected from such a course in general.

While one might not experience any obvious adverse effects from the different kind of teaching, it would be good to know whether my efforts actually made a difference in the end. From the teacher’s point of view, I certainly felt that I was spending my time much more meaningfully than I would have using a more traditional style, and that kept me highly motivated throughout the year. Many students also changed their minds about my methods and gave me praise in private emails and conversations. One student said that I had taught him to write proofs, and claimed that this had helped him in the exams also on other courses. Some physics students thanked me for giving examples of physical applications and for teaching not only the content but also the method of studying mathematics. Another student, who had originally despised my lecturing style, thanked me in the end, saying that during the course he had realised the value of his own work and that this was the most important thing he had learned from the course.

The last mentioned comments show that the methods I employed were about so much more than straightforward delivery of definitions and theorems. The students were taught to read and write mathematics on their own and construct their personal understanding instead of simply memorising results and methods. Although this kind of instruction may be unusual to see in the Durham maths community, I trust that my example shows that, if found valuable, it is fully possible to implement.

Extreme Apprenticeship

|

Since 2011 we have been using the Extreme Apprenticeship method in teaching first year mathematics in the University of Helsinki. The core idea of Extreme Apprenticeship is to support students in becoming experts in their field by having them participate in activities that resemble those of professionals. The main method of teaching is one-on-one instruction, and the students are encouraged to work collaboratively. During the past few years, Extreme Apprenticeship has changed the way the teaching staff and students in our department view learning and teaching.

Extreme Apprenticeship promotes active engagement of the students. Each week, the students start studying a new topic by solving problems given by the teacher. They get as much help as they need from the teaching assistants.

yhteistyoJaLuokka

The teaching assistants do not give answers but guide the students towards solution. They help the students in reading course literature and gaining studying skills. The teaching assistants are undergraduate or graduate students who undergo a training that lasts throughout the semester. Training is important, as teaching in a new way can be very challenging.

The physical learning environment we have created in the middle of our department is an important part of the Extreme Apprenticeship method. It encourages the students to collaborate with each other and interact with the teaching assistants.

ohjausAnnaleena

The students hand in their solutions so that the teaching assistants can read them and give feedback. Emphasis is on learning how to write mathematics, which is very difficult for most students. If the solution is not good enough, the student has an opportunity to improve it. The feedback is two-directional: by reading the students’ answers, the teachers get to know what kind of problems the students have and can react accordingly when planning the tasks and lectures.

tarkistus

After the students have worked on the course assignments, there are lectures. The students have already familiarised themselves with the topic of the lectures by doing the tasks. This is a simple and effective way of making the students prepare for the lectures. The lectures are not for delivering content or going through details. Instead, it is possible to discuss the meaning and consequences of definitions and to address misconceptions. The students do not need to just sit and listen, but they get to work in pairs, discuss with each other and vote on questions posed by the lecturer.

luento

After the lectures, students are given more challenging tasks concerning the topics that have been discussed in the lectures. At the same time, studying a new topic starts with relatively easy tasks.

Compared to traditional teaching, Extreme Apprenticeship has increased student engagement and effort. It has enabled moving from rote learning towards conceptual understanding. Even though the students have to work hard, the feedback from them has been overwhelmingly positive. All in all, the method has had a considerable impact on the atmosphere of our department. The corridors and classrooms are filled with students who solve problems together and talk about maths with excitement and enthusiasm.

XA

Read more:

Rämö, J., Oinonen, L., & Vikberg, T. (2015, February). Extreme Appreticeship – Emphasising conceptual understanding in undergraduate mathematics. Paper presented at the 9th Congress of European research of mathematics education, Prague, Czech Republic.

Rämö, J. & Vikberg, T. (2014). Extreme Apprenticeship – Engaging undergraduate students on a mathematics course. In Proceedings of the Frontiers in Mathematics and Science Education Research Conference 1-3 May 2014, Famagusta, North Cyprus (pp. 26-33).

Hautala, T., Romu, T., Rämö, J. & Vikberg, T. (2012). Extreme apprenticeship method in teaching university-level mathematics. In Proceedings of the 12th International Congress on Mathematical Education, ICME.

Opettaja vai joku ihme hiippari

|

Aloitin pari päivää sitten melontakurssin. Melominen, erityisesti suoraan melominen, on yllättävän hankalaa. Pitää miettiä, missä kulmassa mela menee veteen, säilyttää käsien asento oikeana ja ottaa koko vartalo mukaan. Tämän kaiken miettiminen nostaa otsalle tuskanhien.

Eilen harjoittelimme melomista Seurasaaren ympäristössä. Yksi kurssilaisista kierteli meidän muiden joukossa ja antoi innokkaana neuvoja. Siinä vaiheessa aloin olla jo aika ärsyyntynyt. Kun tämä kaikkitietävä tyyppi tuli neuvomaan minua, urahtelin jotain lyhyttä vastaukseksi ja meloin itsepäisesti eteenpäin.

Vähän myöhemmin tajusin, että kyseessä ei ollutkaan oppilas vaan yksi kurssin ohjaajista. Kukaan ei vain ollut esitellyt häntä minulle, enkä osannut ulkonäöstäkään päätellä häntä opettajaksi. Kyllä nolotti.

Samalla tajusin, miten tärkeää on, että opiskelija tietää, ketkä ovat opettajia. Ja miten tärkeää on, että laitoksemme ohjaajat käyttävät kirkasväristä huomioliiviä.

Liivit ovat olleet meillä käytössä ennen kaikkea sen takia, että opiskelijoilla on matalampi kynnys kysyä kysymyksiä, kun heidän ei tarvitse arvuutella, kuka on ohjaaja. Toisaalta suuri osa ohjaajistamme on itsekin opiskelijoita, ja liivin pukeminen auttaa heitä siirtymään opettajan rooliin. Nyt liivien käytölle tuli vielä yksi perustelu lisää: liivistä opiskelija tietää, että häntä lähestyvä henkilö on opettaja eikä joku ihme hiippari. Keskustelu ja vuorovaikutus sujuvat paljon paremmin, jos opiskelija tietää puhuvansa opettajan kanssa.

kaytava

Harjoitustehtävät kisällioppimisessa – esimerkkejä lineaarialgebran kesäkurssilta

|

Opetin touko-kesäkuussa Helsingin yliopiston Avoimessa yliopistossa kisällioppimisen menetelmää soveltaen kurssin Lineaarialgebra ja matriisilaskenta I. Kisällioppimisessa yhtenä perusajatuksena on tekemällä oppiminen, minkä vuoksi harjoitustehtävien laatimiseen oli kiinnitettävä erityistä huomiota. Kisällioppimisessa harjoitukset pyritään suunnittelemaan niin, että tehtävät

  • kattavat kurssin keskeiset asiat mahdollisimman hyvin
  • ohjaavat opiskelijan selvittämään asioita itse kurssimateriaalin avulla
  • kiinnittävät opiskelijan huomion oppimisen kannalta oleellisiin seikkoihin
  • mahdollistavat opiskelijan oman oivalluksen
  • ovat asteittain vaikeutuvia
  • sisältävät sopivasti kertausta.

Lisätietoa kisällioppimisesta löytyy blogikirjoituksesta “Kisällioppiminen“.

Katsaus harjoitustehtäviin

Alla esiteltävät harjoitustehtävät eivät syntyneet tyhjästä tälle kesäkurssille, vaan ne ja niiden johdatteleva tyyli perustuvat aikaisempien kurssitoteutusten tehtäviin, jotka sain käyttööni Jokke Häsältä ja Johanna Rämöltä.

Harjoitus 1

Kurssin ensimmäinen tehtävä ohjasi opiskelijat heti kurssimateriaalin pariin. Ajatuksena oli, että opiskelijat pääsevät itse tekemään niitä asioita, joista kurssimateriaalissa puhutaan. Osalle kurssin opiskelijoista tehtävä oli helposti lähestyttävä lämmittelytehtävä; toisille opiskelijoille hyvinkin tarpeellista kertausta muun muassa koordinaatiston piirtämisestä ja pisteen merkitsemisestä koordinaatistoon.

h1t1

Lineaarikombinaation käsitteeseen liittyvä vektorien virittämän aliavaruuden käsite on monille opiskelijoille opintojen alkuvaiheessa haasteellinen. Tämän vuoksi näiden käsitteiden pohjustaminen aloitettiin heti ensimmäisessä harjoituksessa. Alla näkyvän tehtävän 7 b-kohta sai monet palaamaan lineaarikombinaation määritelmään ja toimi mainiosti kysymysten herättäjänä.

h1t6-7

Ensimmäisen harjoituksen lopussa pohjustettiin vektorien virittämän aliavaruuden käsitettä yhdistämällä lineaarikombinaation käsite span-merkintään:

h1t18-19

Harjoitus 2

Tehtävässä 1 kerrattiin lineaarikombinaation käsitettä ja harjoiteltiin määritelmän käyttöä:

h2t1

Tehtävissä 5 ja 6 harjoiteltiin span-merkintää yksinkertaisissa, konkreettisissa tilanteissa:

h2t5

h2t6

Tehtävässä 9 opeteltiin etsimään aliavaruudelle virittäjävektorit tietynlaisessa tilanteessa. Tätä taitoa tarvittiin myöhemmin vaativampien tehtävien yhteydessä.

h2t9

Harjoitus 3

Vektorien virittämän aliavaruuden käsitettä, siihen liittyviä merkintöjä ja geometrisia näkökulmia kerrattiin tehtävässä 1:

h3t1

Tehtävissä 8-10 lineaarikombinaation ja virittämisen käsitteitä tarvittiin kannan käsitteen opiskelun yhteydessä:

h3ts3

Harjoitus 4

Tehtävissä 5 ja 7 virittäminen ja lineaarikombinaatiot esiintyvät kannan ja koordinaattien opiskelun yhteydessä. Tehtävä 6 on abstraktimpi vektorien virittämään aliavaruuteen liittyvä tehtävä. Näissä tehtävissä tarvittavia taitoja oli jo harjoiteltu edellisillä viikoilla, mikä auttoi opiskelijoita pääsemään niissä alkuun. Toisaalta opiskelijat saivat näissä tehtävissä kerrata aikaisemmin opiskelemiaan asioita ja soveltaa niitä laajemmissa kokonaisuuksissa.

h4ts2

Kurssin osallistujat ja rakenne

Kurssille ilmoittautui 132 opiskelijaa. Heistä suurin osa oli Helsingin yliopiston perustutkinto-opiskelijoita, jotka lukivat matematiikkaa sivuaineenaan. Kurssi kesti viisi viikkoa ja siihen kuului viisi harjoitustehtäväkokoelmaa, joissa kussakin oli 15-19 tehtävää. Opiskelijat palauttivat tekemiensä tehtävien ratkaisut viikoittain kirjallisesti, mutta niitä ei tarkastettu. Harjoituksia teki kurssin aikana 97 opiskelijaa.

Luentoja oli yhteensä 24 tuntia, 2-3 kertaa viikossa kaksi tuntia kerrallaan. Lisäksi kurssiin kuului 17 harjoitustuntia, joiden aikana opiskelijat saivat tehdä tehtäviä omassa tahdissaan itsenäisesti tai toistensa kanssa. Paikalla olevilta ohjaajilta oli tällöin mahdollista kysyä neuvoa. Harjoitustunneille osallistui kurssin aikana 50 eri opiskelijaa, joista osa oli paikalla lähes joka kerta ja osa silloin tällöin. Kurssilla oli vastuuopettajan lisäksi yksi harjoitusohjaaja.

Kurssikokeeseen ja kahteen uusintakokeeseen osallistui yhteensä 81 eri opiskelijaa, joista 74 sai kurssin suoritettua. Kurssin sisällöstä ja käytännöistä löytyy lisätietoa kurssin sivulta.

Piirretään pöytiin!

|

Saimme tällä viikolla uudet pinnat pöytiimme. Nyt pöytään piirtäminen on entistä helpompaa!

Olemme  kirjotelleet pöytiin jo reilun parin vuoden ajan. Niin opiskelijoiden kuin opettajienkin on paljon helpompi selittää ajatuksiaan, kun samalla voi piirtää pöytään kuvia ja kaavoja. Pöydät kannustavat yhteistyöhön ja vuorovaikutukseen.

kaytava_pieni

Kokeilu alkoi pleksilevyillä. Pöydän päälle laitettu akryylilevy muuttaa pöydän tussitauluksi, johon voi piirtää taulutusseilla. Levyt ovat edullisia, ja lisäksi läpinäkyvän levyn alle on kätevä laittaa esimerkiksi koordinaatistoruudukko. Ongelmana on kuitenkin se, että tussinjäljet tuppaavat jumahtamaan kiinni pleksilevyn pintaan ja niitä saa välillä hinkkailla melkoisella antaumuksella.

Seuraava askel oli pöydän päälle laitettava valkotaulu. Teetimme tauluja, jotka ovat juuri sen kokoisia, että kun taulun laittaa pöydän päälle, taulun reunat pitävät levyn paikoillaan. Tauluja on helppo pyyhkiä, mutta kuminpurut ja muut roskat kertyvät hieman sotkuisesti reunan väliin. Lisäksi taulun kulmat eivät kestä niihin osuvia kolhuja, ja kulmista putoilee osia.

Nyt hankitut uudet pöytälevyt ovat myös valkotauluja, mutta niissä ei ole enää erillistä reunusta. Taulut kiinnitettiin pöytiin kaksipuoleisella teipillä. Levyt ovat tosin niin painavia, että ne olisivat pysyneet paikoillaan varmaan vähemmälläkin (esim. liukuestematolla).

Hyvin toimii!

poikaPiirtaa

 

Kisällioppiminen

|

Kirjoittajina Johanna Rämö ja Thomas Vikberg

Olemme parin viime vuoden aikana yrittäneet muuttaa matematiikan kursseja vastaamaan paremmin opiskelijoiden tulevaa arkea. Matematiikka työkseen tekevät eivät istu joka päivä tuntitolkulla kuuntelemassa matemaattisia esityksiä, vaan he painiskelevat itse matematiikan kanssa. Tämä näkyy myös siinä miten he oppivat uutta matematiikkaa, tai kuten laitoksemme johtaja totesi syksyllä 2011, “Matematiikkaa ei opi kuuntelemalla eikä lukemalla, vaan ainoastaan tekemällä”.

Olemme tätä varten kehittäneet isoilla LuK-kursseillamme nk. tehostetun kisällioppimisen menetelmää. Menetelmä on alun perin luotu vastaamaan modernin ohjelmistokehityksen opetuksen haasteisiin Helsingin yliopiston tietojenkäsittelytieteen laitoksella (jossa sitä kutsutaan toisinaan pajaopetukseksi). Oman laitoksemme opetuksessa menetelmää on kehitetty matematiikan opetukseen sopivaan muotoon. Tiivistäisimme tehostetun kisällioppimisen kolmeen ideaan:

  1. Opiskelijat ottavat aktiivisen roolin omassa opiskelussaan.
  2. Opiskelijoiden opiskelua tuetaan.
  3. Palaute kulkee opettajan ja opiskelijoiden välillä, jolloin kaikilla on realistinen kuva siitä, mitä opiskelijat osaavat.

Opetuskokeilu ei ole ollut pientä “kokeilua”, vaan kurssit, joita olemme muokanneet, ovat suuria. Esimerkiksi tämän syksyn lineaarialgebran kurssia on aktiivisesti suorittanut 375 opiskelijaa ja keväällä tarkoituksena on järjestää neljä suurta kurssia menetelmää käyttäen. Opiskelijoiden joukossa on tulevia matemaatikoita, soveltavia matemaatikoita, opettajia ja sivuaineilijoita.

Mitä tämä käytännössä tarkoittaa

Vielä pari vuotta sitten, opiskelijat istuivat luennolla kurssista riippuen 4-5 tuntia viikossa. He tekivät laskuharjoitustehtäviä itsekseen, ja istuivat laskuharjoitusten esittelytilaisuudessa kaksi tuntia viikottain saamassa oikeat vastaukset tehtäviin. Kisällioppimisessa opiskelijat tekevät enemmän tehtäviä ja istuvat vähemmän luennolla. Ennen tehtävät liittyivät luentoihin, nykyään luennot liittyvät tehtäviin. Esimerkiksi tänä syksynä opiskelun tahti on näyttänyt tältä:

  1. Kurssin uusi asia esitetään helpohkojen tehtävien avulla, joita opiskelijat saavat tehtäväkseen.
  2. Suoriutuakseen tehtävien ratkaisemisesta, opiskelijan on luettava kurssimateriaalia itsekseen, mutta halutessaan hän saa opettavalta tiimiltä yksilöllistä ohjausta.
  3. Kun opiskelijat ovat työstäneet uutta asiaa ratkomalla siihen liittyviä tehtäviä, asiaa käsitellään luennoilla seuraavalla viikolla.
  4. Samaisella viikolla opiskelijat saavat tehtäväkseen vaikeampia tehtäviä aiheesta, jota käsitellään luennoilla

Opettava tiimi, joka koostuu assareista ja yliopisto-opettajista, ohjaa opiskelijoita heidän tarpeidensa mukaan. Ohjaus on henkilökohtaista, ja jokainen opiskelija saa apua juuri niissä asioissa, jotka ovat hänelle vaikeita. Valmiita vastauksia ei anneta, vaan opiskelijaa ohjataan oivaltamaan asiat itse. Opiskelijat siis ”pakotetaan” opiskelemaan asiat kurssimateriaalista tehtäviä tehden. Kun he ovat tutustuneet uuteen aiheeseen itse ohjaajien avustuksella, aiheesta keskustellaan luennolla. Tässä apuna ovat sähköiset äänestykset, joiden avulla opiskelijat voivat kertoa vastausehdotuksiaan ja mielipiteitään keskusteltuaan ensin vieruskaverinsa kanssa. (Lisätietoa tästä löytyy blogikirjoituksesta ”Täyskäännös”.)

Yksi kisällimenetelmän kulmakivistä on palautteen antaminen ja saaminen. Osa opiskelijoiden kirjallisesti palauttamista tehtävät tarkistetaan viikoittain, jolloin opettava tiimi saa tietää, mitä opiskelijat todella osaavat. Käsityksemme opiskelijoiden osaamisesta on nykyään huomattavasti realistisempi kuin ennen. Opiskelijat puolestaan saavat tehtäviä palauttamalla jatkuvaa palauttetta työstään. He saavat myös korjata ratkaisujaan. Virheistä ei siis rankaista, vaan niistä opitaan. Kisällioppiminen vaatii aivan erilaisia opetustiloja kuin perinteinen opetus, jossa opettaja luennoi edessä ja opiskelijat istuvat riveissä hiljaa kuunnellen. Olemme joutuneet miettimään tilaratkaisut uusiksi, jotta ne tukisivat niin kisälliopetusta kuin muitakin opiskelijalähtöisiä opetusmenetelmiä. (Lisätietoa tästä löytyy blogikirjoituksesta ”Tavoitteena oppimisyhteisö”.)

Vanhaan ei ole paluuta

Nautimme kisällimenetelmällä opettamisesta emmekä halua enää palata vanhaan opetustapaan. Tunnemme todella vaikuttavamme opiskelijoiden oppimiseen ja saamme nähdä onnistumisen elämyksiä päivittäin.