Kuuluisan saksalaisen matemaatikon Carl Friedrich Gaussin (1777–1855) kerrotaan hämmästyttäneen opettajaansa jo 9-vuotiaana matemaattisilla kyvyillään. Tarinan todenperäisyys on kuitenkin kaikkien historiallisten anekdoottien tapaan epäselvä. Tarinaa ja sen taustalla olevaa matematiikkaa on käsitelty mm. Matematiikkalehti Solmussa [1]. Tässä kirjoituksessa tarkastelen Gaussin (mahdollisesti) opettajaltaan saamaa tehtävää erilaisten näkökulmien — matematiikan eri ”maailmojen” — kautta.
Gaussin tehtävä
Gaussin kerrotaan olleen jo koulussa etevä laskija, ja opettaja joutuikin antamaan pienelle matemaatikonalulle runsaasti lisätehtäviä. Eräänä päivänä Gauss oli jälleen tehnyt kaikki annetut harjoitustehtävät, jolloin kyllästynyt opettaja käski hänen laskea yhteen kaikki kokonaisluvut yhdestä sataan eli summan 1 + 2 + 3 + … + 99 + 100. Opettaja tietysti odotti, että näin pitkän laskun laskeminen kestäisi jopa etevältä Gaussilta melko kauan, mutta eipä aikaakaan, kun Gauss oli kirjoittanut vastaukseksi 5050. Emme voi varmasti tietää, mitä Gauss oli ajatellut (jos kerrottu tarina on totta). Todennäköisesti hän oli keksinyt ”parittaa” yhteenlaskettavia seuraavasti:
1 + 2 + 3 + 4 + … + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) + … + (50 + 51).
Silloin jokaisen parin summa on 101, ja pareja on yhteensä 50 kappaletta. Näin ollen tuloksen on oltava 50 * 101 = 5050. (Tämä päättely toimii, koska yhteenlaskettavia oli parillinen määrä.) Tulos voidaan yleistää koskemaan kaikkia luonnollisia lukuja (eli johtaa ”laskukaava” sille, miten lasketaan yhteen n kappaletta peräkkäisiä luonnollisia lukuja). Se, miksi tietty ”laskukaava” toimii, voi näyttäytyä meille monella eri tavalla. Mietinkin siis seuraavaksi edellistä esimerkkiä eri ”matematiikan maailmojen” näkökulmasta.
David Tallin matematiikan kolme maailmaa
Ajatellessamme matemaattisesti pyörittelemme usein – kuten äsken – numeroita ja muita matemaattisia symboleita. Toisaalta Gaussin saamaa laskutehtävääkin voisi symbolismin sijasta lähestyä myös konkretian tai formaalin matemaattisen teorian kautta. Nämä eri matemaattisen ajattelun aspektit ovat David Tallin matematiikan kolmen maailman näkökulman lähtökohdat [3]. Tallin jaottelu ei ole filosofinen positio tai teoria siitä, mitä matematiikka on, vaan yksinkertainen viitekehys sille, minkälaiset ajattelun aspektit ovat tai voivat olla läsnä, kun ihminen oppii matematiikkaa. Tallin matematiikan kolme maailmaa ovat
- käsitteellis-ruumiillinen/ilmenevä maailma (conceptual-embodied)
- proseptuaalis-symbolinen maailma (proceptual-symbolic) ja
- aksioomaattis-formaali maailma (axiomatic-formal).
Pyrin seuraavaksi avaamaan, mihin nämä vaikeat sanat viittaavat. Gaussin tehtävää aluksi miettiessäni päädyin siihen, että summa 1 + 2 + 3 + … + 100 on sama kuin 50*101. Luku 50 on puolet sadasta ja 101 on sama kuin 100+1. Yleisemmin voidaankin laskea n peräkkäistä luonnollista lukua yhteen kaavalla
}{2}) .
.
Miten tämä matemaattinen totuus voi meille näyttäytyä tai miten sen voi keksiä? Tallin ensimmäisen maailman näkökulmasta se voi näyttäytyä esimerkiksi seuraavanlaisen kuvan avulla.
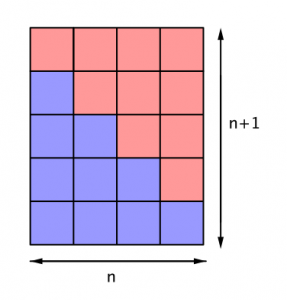
Kuvassa summa 1 + 2 + 3 + 4 ruumiillistuu ja ilmenee punaisten tai sinisten ruutujen lukumääränä. Koska ruutuja on yhteensä 4*5 kappaletta ja lisäksi sinisiä ja punaisia ruutuja on yhtä paljon, on summan 1 + 2 + 3 + 4 pakko olla puolet tulosta 4*5. Voimme ”sielumme silmin” nähdä, että olipa ruutujen määrä mikä tahansa (n kappaletta), havaintomme pysyy samana: yhtälön
}{2})
on pakko olla totta. Tallin ensimmäisessä maailmassa on siis kyse siitä, että matematiikkaa ymmärretään asioiden konkretisoituessa tavalla tai toisella (esineet, kuvat, mielikuvat, kehollinen kokeminen…). Tällaiset matematiikkakokemukset ovat mm. Varga–Neményi-menetelmän (eli ns. unkarilaisen matematiikan) ydintä [4].
Toisaalta asiaa voi ajatella symbolisesti Tallin toisen maailman näkökulmasta esimerkiksi merkitsemällä S = 1 + 2 + 3 + … + n ja ”laskemalla allekkain”:
%20+%20n)
%20+%20\dots%20+%20~%1E~~%202%20~%1E~~%20+%20~~~%201%20~%1E~~)
________________________________________________
%20+%20(n+1)%20+%20\dots%20+%20(n+1)%20+%20(n+1)}_{n%20\text{%20kpl}})
Siis on oltava 2S = n(n+1), mikä tarkoittaa että S = n(n+1)/2. Tämä matematiikan maailma näyttäytyy usein koulun matematiikan tunneilla ja myös korkeakouluissa matematiikkaa opiskellessa. Maailman nimessä esiintyvä sanaleikki ”prosepti” viittaa sanoihin process ja concept; ajattelemme symboleita pyöritellessämme sekä yhteenlaskun prosessia että lukujen yhteenlaskua käsitteenä.
Mikä sitten on Tallin kolmannen maailman näkökulma esiteltyyn summakaavaan? Aksiomaattis-formaalissa maailmassa katsotaan nimensä mukaisesti matematiikkaa siitä näkökulmasta, mikä olisi ns. formalistisen matematiikkakuvan mukaista matematiikkaa: matematiikka perustuu sovittuihin aksioomiin, joista johdetaan deduktiivisesti uutta tietoa. Tässä tarkasteltava väite koskee matemaattisen teorian näkökulmasta luonnollisten lukujen joukkoa. Luonnolliset luvut määritellään matemaattisessa teoriassa esimerkiksi ns. Peanon aksioomien avulla. Summakaavan väite voitaisiin formaalisti todistaa induktiotodistuksella, sillä Peanon aksioomissa on mukana ns. induktioaksiooma. Väite todistettaisiin toteamalla aluksi, että väite E(n), joka on yhtälö 1+2+3+4+…+n = n(n+1)/2 pätee, kun n=1. Tämä on itse asiassa melko helppo huomata, sillä
}{2}) .
.
Tämän jälkeen todistettaisiin lause E(n) => E(n+1) (eli jos väite pätee arvolla n, niin se pätee myös arvolla n+1). Tämän jälkeen induktioaksiooman perusteella tulos pätee kaikilla luonnollisilla luvuilla. Käyn läpi seuraavaksi myös myös ”jossittelulauseen” E(n) => E(n+1) todistuksen.
Oletetaan, että
}{2}) .
.
Tällöin
}{2}}%20+%20(n+1)%20=%20\frac{n(n+1)}{2}%20+%20(n+1)%20\\%20~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=%20\frac{n(n+1)+2(n+1)}{2}%20\\%20\\%20~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=%20\frac{(n+2)(n+1)}{2}%20\\%20\\%20~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=%20\frac{(n+1)(n+2)}{2}%20\\%20\\%20~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=%20\frac{(n+1)((n+1)+1)}{2}) .
.
Tallin ensimmäisessä ja toisessa maailmassa jouduin turvautumaan “potentiaalisesti äärettömiin” todistuksiin saadakseni itseni vakuuttuneeksi kaavan oikeellisuudesta. Aksiomaattis-formaalissa maailmassa todistus on “äärellinen” ja tuloksen yleistyminen kaikkia luonnollisia lukuja koskevaksi (vaikken jokaista tapausta voi koskaan erikseen käydä läpi) selittyy sillä, millaiseksi luonnollisten lukujen joukko ymmärretään matematiikan teoriassa.
Matematiikan kuusi osaa ja vuoropuhelu
Mikä äsken esitellyistä näkökulmista sitten on oikea tapa ajatella asiaa? Mielestäni mikään tapa ei ole sen enempää ”oikea” kuin toinen, vaan nämä kaikki voivat olla läsnä ajattelussamme. Puhuttaessa matemaattisesta ajattelusta ei tarvitse (eikä ehkä ole edes hyötyä) ottaa kantaa siihen, mitä matematiikka ontologisessa mielessä on, eli ovatko esimerkiksi matemaattiset oliot olemassa ”tuolla jossakin” (platonismi) vai onko matematiikka vain sääntöjä ja merkkijonoja (formalismi). Toimintamme on siitä riippumatta samanlaista.
Juha Oikkonen on ehdottanut Tallin kolmen maailman rinnalle matematiikan kahta puolta, jotka ilmenevät, kun matematiikkaa tehdään ”tässä ja nyt” [2]. Oikkonen jaottelee matematiikan sosiaalis-subjektiiviseen ja objektiivis-formaaliin puoleen. Oikkosen näkemys on, että matematiikan tekeminen on (parhaimmillaan) jatkuvaa vuoropuhelua näiden kahden puolen välillä. Kahtiajako yhdistettynä Tallin kolmijakoon näyttäisi itse asiassa tuottavan mielenkiintoisen ”matematiikan kuuden osan” näkökulman.
Jos piirrän Tallin ensimmäiseen maailmaan kuuluvan kuvan ymmärtääkseni summakaavan, on samaan aikaan käsissäni jotain objektiivista ja jotain subjektiivista. Kuva on objektiivinen siinä mielessä, että kaikki voivat sitä havainnoida ja se on muuttumaton. Toisaalta se, miten kuvassa nähdään matemaattisia ideoita, on subjektiivista. (Lukija voi vielä vilkaista kuvaa, jossa oli sinisiä ja punaisia ruutuja ja miettiä, millä tavoilla matemaattinen idea siinä näkyy.) Näin Tallin ensimmäisen maailman ilmiöt voidaan nähdä jakautuvan kahtia.
Tallin toiseen maailmaan kuuluvat laskusäännöt ovat jotain täysin objektiivista ja esimerkiksi aiemmin kirjoittamani laskut ovat siis objektiivisesti tosia. Toisaalta myös symboliseen toimintaan liittyy sosiaalis-subjektiivinen puoli; mm. oppijoiden muodostamat miniteoriat (eli ”omat laskusäännöt”) tuntuvat selvästi kuuluvan tähän. Miniteoriassa voi olla kyse esimerkiksi “väärästä yleistyksestä”. Koska
%20=%202x+2y) ,
,
voisi paremman tiedon puuttuessa tulla ajatelleeksi että pätee myös
^2%20=%20x^2+%20y^2) .
.
Tällaiset miniteoriat ovat luonteeltaan vahvasti subjektiivisia: oppija rakentaa ne itse.
Aksiomaattis-formaaliin maailman taas ajattelisi olevan oikeastaan täysin objektiivista. Mutta myös siihen liittyy sosiaalis-subjektiivinen puoli. Tätä edustaa esimerkiksi matemaatikkojen strateginen metatason keskustelu: ”Voisimme käyttää ajatuksia X,Y ja Z asian Ö todistamiseksi.” Esimerkiksi tällainen keskustelu on osa matematiikan tekemisen (sosiaalis-subjektiivista) prosessia erona objektiivisille matemaattisille tuloksille.
Kaikkein opettavaisinta tässä kaikessa lienee se, että matemaattisen ajattelun ja keksimisen prosessi voi liikkua useilla eri tasoilla. On monta tapaa ”kokea matematiikkaa” ja tehdä sitä itselleen ja muille mielekkääksi. On sääli, jos koulussa matematiikan oppiminen jää pelkäksi merkityksettömäksi symbolien pyörittelyksi.
Viitteet:
[1] Matematiikkalehti Solmu. http://solmu.math.helsinki.fi/2008/diplomi/gauss.pdf (13.3.2013)
[2] Oikkonen, J. (2004). Mathematics between its two faces, Matemaattisten aineiden opettajan taitotieto – haste vai mahdollisuus, L. Jalonen, T. Keranto and K. Kaila (toim.), University of Oulu, Finland, pp. 23-30, ISBN 951-42-7886-0.
[3] Tall, D. (2004). Thinking through three worlds of mathematics, Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, Bergen, Norway, 4, 281–288.
[4] Varga–Neményi – yhdistys ry. http://www.varganemenyi.fi/includes/menetelma.php (13.3.2013)
