Kirjoittajat: Kia Lindqvist, Jokke Häsä, Johanna Rämö
Kurssilla Algebralliset rakenteet I kokeiltiin keväällä 2020 uutta opetusmenetelmää korvaamalla luennot ohjatulla ryhmätyöskentelyllä. Opetusmuodon tavoitteena oli tukea opiskelijoiden aktiivista roolia, yhteistyötaitojen kehittymistä sekä yhteisöllisyyttä.
Aiemmin ongelmana oli, että perinteisillä opettajajohtoisilla luennoilla opiskelijoiden keskittyminen oli heikkoa ja he helposti passivoituivat. Toisaalta aktivoivat ja opiskelijakeskeiset luennot eivät olleet kaikkien opiskelijoiden mielestä merkityksellisiä. Lisäksi kehittyvä verkko-opetus mahdollisti sen, että kampukselle ei ollut enää pakko tulla, eivätkä etäopiskelijat saaneet tukea ryhmä- ja kommunikaatiotaitojensa kehittämiseen. Näihin ongelmiin pyrittiin hakemaan ratkaisua korvaamalla luennot prime time -ohjatulla ryhmätyöskentelyllä.
Ryhmätyöskentely rakennettiin kurssin jo olemassa olevien opetusmenetelmien päälle, eli kurssilla oli vahvasti läsnä tehostetun kisällioppimisen menetelmä. Opiskelijat opiskelivat kurssin aiheita edelleen kurssikirjaa lukemalla ja tehtäviä tekemällä. Näihin molempiin sai apua avoimesta oppimistilasta, jossa kurssin opettajat päivystivät. Osasta tehtävistä sai automaattista palautetta Moodle-järjestelmältä, osasta taas opettajat antoivat palautetta.
Ryhmätyötä varten opiskelijat jakautuivat kurssin alussa noin 6 hengen ryhmiin. Ryhmät tapasivat joka viikko itsenäisesti ja tekivät heille annettua ryhmätehtävää, joka oli kurssin aiheita soveltava laajahko tehtävä. Ryhmätehtäviä oli kurssin aikana kaksi. Opiskelijat osallistuivat ryhmänsä kanssa viikoittaiseen pakolliseen opetustuokioon, jonka veti kurssin vastuuopettaja yhdessä apuopettajan kanssa. Yhteisen alustuksen jälkeen jokainen ryhmä sai 15 minuutin ajan keskustella ryhmätehtävästä jommankumman opettajan kanssa. Keskustelussa opettaja tuki matematiikan oppimisen lisäksi hyvien ryhmätyöskentelyn käytänteiden muotoutumista.
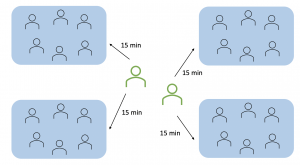
Opetustuokioissa kukin ryhmä keskusteli opettajan kanssa 15 minuuttia ryhmätehtävästä. Sillä välin muut ryhmät tekivät muita tehtäviä opettajan ohjeistuksen mukaisesti.
Kurssin arviointi oli suunniteltu siten, että se tuki ryhmien yhteistoimintaa. Osa kurssin arvosanasta muodostui ryhmätehtävistä, joten niiden tekemiseen oli panostettava. Jotta ryhmän kaikki jäsenet työskentelisivät oman oppimisensa eteen eikä syntyisi vapaamatkustajan ongelmaa, ryhmätyöstä saatavat pisteet jaettiin ryhmän jäsenille sen mukaan, miten he suoriutuivat yksilöinä jälkikäteen suoritettavista lyhyistä osaamistesteistä. Lisäksi, jotta ryhmä ponnistelisi kaikkien jäsentensä oppimisen eteen, ryhmällä oli mahdollisuus saada bonuspisteitä, jos kaikkien jäsenten osaamistestien yhteenlaskettu pistemäärä oli riittävän korkea.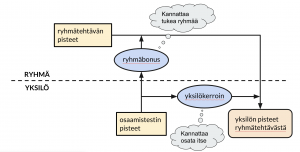
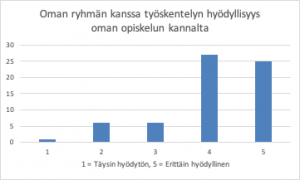
Kurssin lopussa teetetty palautekysely sekä opiskelijoiden kirjoittamat yksilöpohdinnat ryhmätöiden onnistumisesta tuovat esiin opiskelijoiden kokemuksia uudesta opetusmuodosta. Suurin osa opiskelijoista koki ryhmätyöskentelyn positiivisena lisänä kurssille. Erityisesti oman ryhmän kanssa työskentely koettiin hyödyllisenä oman oppimisen kannalta.
Opiskelijat esittivät yksilöpohdinnoissaan esimerkiksi seuraavanlaisia huomioita ryhmänsä merkityksestä:
”Ryhmätehtävissä erityisesti mahtavaa on ollut se, että jokaisella ryhmän jäsenellä on oma tapansa ajatella ja itse ainakin olen oppinut kurssin asiat paremmin.”
”Jotkut asiat ovat olleet toisille helpompia ja toisille vähän vaikeampia ymmärtää. Tälläisissä tilanteissa paremmin ymmärtävä henkilö on selittänyt heikommin ymmärtävälle henkilölle. Molemmat oppivat samalla, yksi oppii miten selitetään asioita toiselle ja toinen ymmärtää asian mitä ei aiemmin ymmärtänyt.”
”Ryhmätyöstä nauttiminen oli suurin positiivinen saavutus kurssilta. Tulevaisuutta ajatellen uskon opiskelevani enemmän ryhmässä ja käyttävän siitä saatavat edut paremmin hyödyksi.”
Molemmissa ryhmätehtävissä ryhmiä kannustettiin valitsemaan jokaiselle ryhmän jäsenelle rooli. Ryhmän roolit mahdollistivat ryhmän jäsenten välisen työnjaon ja loivat järjestystä ja ennustettavuutta ryhmän toimintaan. Opiskelijat suhtautuivat rooleihin vaihtelevasti – osa piti niitä hyödyllisinä alusta alkaen, osa ei lämmennyt rooleille lainkaan ja osa muutti suhtautumistaan kurssin aikana. Roolien suhteen havaittiin tärkeäksi hyvä ohjeistus, opiskelijoiden motivoiminen roolien käyttöön sekä rooleista keskusteleminen opiskelijoiden kanssa useasti kurssin aikana. Opiskelijat kuvasivat roolien hyödyllisyyttä muun muassa seuraavasti:
”Oli helpottavaa esimerkiksi tukeutua rooliin, jotta uskalsi sanoa asioita uusien ihmisten seurassa.”
”Ensimmäisessä ryhmätyössä roolit ei herättänyt positiivisia tunteita, joten asenne niitä kohtaan ei ollut parhaimmasta päästä. Toisessa ryhmätyössä yritin tätä vähän paremmalla asenteella ja lopputulos oli myös sen mukainen. Roolit paransivat mielestäni ryhmätyötä yleisesti”
”Moni meistä on varmasti jo tehnyt paljo ryhmätöitä ja roolien miettiminen ryhmässä tuntui harvinaisen typerältä, eikä ainakaan kukaan meidän ryhmässä nähnyt siitä mitään hyötyä.”
Kurssipalautteessa opiskelijat toivat esiin sen, että automaattista palautetta antavat tehtävät tutustuttivat hyvin uuteen aiheeseen ja ryhmätehtävässä pääsi soveltamaan ja kertaamaan näitä taitoja. Eräs opiskelija kuvasi ryhmätehtäviä seuraavasti:
”Usein tehtyäni tehtäviä jostakin aiheesta ensimmäisen kerran ymmärrän aiheen sen verran että onnistun niissä, mutta tarvitsen vielä lisää harjoitusta jotta ymmärrys juurtuisi, ja tämä ryhmätehtävä ajoi juuri sitä roolia oppimisessani.”
Uusi opetusmuoto ja sen sisältämä läsnäolopakko saivat opiskelijat saapumaan paikalle. Opiskelivat myös tekivät tehtäviä yhdessä ryhmän kanssa opetustapaamisten ulkopuolella. Nekin, jotka olivat aiemmin saattaneet opiskella ainoastaan yksin, pääsivät ryhmätyön kautta ratkomaan tehtäviä yhdessä. Eräs sivuaineenaan matematiikkaa lukeva kuvasi ryhmätyöskentelyn hyötyjä oman opiskelunsa kannalta seuraavasti:
”Päädyn usein puurtamaan matematiikan opintojeni kanssa yksin, mutta tämän kurssin kautta olen tutustunut ihmisiin, joiden kanssa voin vaikka viestitellä, jos jotkin tehtävät mietityttävät.”
Opiskelijoilla olikin kurssin aikana rikkaita keskusteluja sekä keskenään että opettajan kanssa, minkä lisäksi opettaja pääsi seuraamaan kaikkien opiskelijoiden oppimisprosessia läheltä ja tukemaan sitä. Kurssin suurimpia onnistumisia olivat juuri avoimet ja innostavat keskustelut sekä konkreettinen yhdessä tekeminen.
Tässä kirjoituksessa esitetyt uutta opetusmetodia koskevat tulokset ja opiskelijoiden kokemukset esiteltiin ensimmäisen kerran Pedaforum 2020 -konferenssissa 21.8.2020.