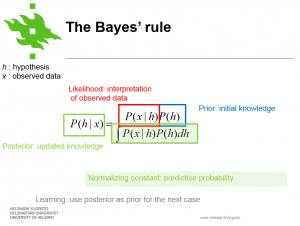
Bayesin teoreema (myös Bayesin sääntö tai Bayesin laki) on ehdolliseen todennäköisyyteen liittyvä matemaattinen teoreema. Teoreeman voidaan tulkita kuvaavan käsitysten päivittämistä uuden todisteaineiston valossa, eli priorin päivittämistä datan ja mallin avulla posterior-tiedoksi. Tutkittaessa asiaa myöhemmin uudestaan: vanha posterior-tieto voidaan käyttää uutena priorina.
Priori kuvaa alkukäsitystä tutkittavasta asiasta, eli meidän tapauksessamme arviota mereen vaeltavien smolttien määrästä. Saimme asiantuntija-arvion Vesi- ja Kalatutkimus Oy:ltä. Heidän arvion mukaan mereen vaeltaisi n. 5000 taimensmolttia. Käsityksemme populaatiosta on normaalistijakautunut. Arvioon sisältyi reilusti epävarmuutta ja siksi hajonta määräytyi 3000.
Alla priori koodin pätkänä.
model {
#P(N)
# N = ‘True number of leaving trouts this year’
N<-round(cN)
cN~dnorm(5000, prec_N)I(1,)
prec_N<-pow(sd_N, -2)
sd_N<-3000
Veden lämmetessä kahdeksaan asteeseen, smoltit aktivoituvat ja lähtevät vaeltamaan merta kohti. Veden lämpötila oli datan keräämisen alkuhetkellä (9.4.2015) 4,2 astetta. Oletamme lämpötilan nousevan muutamassa viikossa 8 asteeseen, joten vaelluksen huippu ajoittuisi datan keruun alkupuolelle. Tällä oletuksella päädyimme käyttämään lognormal jaukaumaa.
Alla pätkä mallin koodista
#P(p[i])
# p[i] = ‘Daily probability of leaving’.
# We can use any function p = f(i) that satisfies:
# 1) sum(p) = 1
# Here we use a scaled version of lognormal density
for(i in 1:m) {
pi[i] <- (1/i)*exp(- pow(log(i)-location, 2) / scale)
p[i] <- pi[i] / sum(pi[1:60])
# Number of leaving trouts at day i
n[i]~dbin(p[i],N)
# Priors for the distribution of p
myy_p~dnorm(25,tau_myy)I(0.01,)
tau_myy<-pow(7,-2)
sd_p~dnorm(10, tau_sd)I(0.01,)
tau_sd<-pow(5, -2)
scale <- log(1 + pow(sd_p/myy_p,2) )
location <- log(myy_p) -0.5*scale
Mereen vaeltavien smolttimäärien arvio perustuu Vesi- ja Kalatutkimus Oy:n tekemään merkitse ja takaisinpyynti metodiin. Merkityillä smolteilla saadaan myös päivitettyä pyydysten/pyydyksen tehoa. Pyydyksen tehoa arviotiin selvittämällä sille priori. Priori selvitettiin vapauttamalla 100 mandariinia joen ylävirtaan, joista 70 meni patouomaan, 20 jäi kalatieuomassa olevaan ruuviin, ja 10 meni kalatieuomassa ruuvin ohi (kts. kuva).
Mallissamme pyydys noudattaa betajaukaumaa, jossa pyydyksen teho saa todennäköisyysarvon nollan ja yhden väliltä. Mikäli merkitty kala pyydetään uudestaan merkitään se koodissa onnistumiseksi(alpha). Jos kala ei päädy pyydykseen uudestaan, merkitään se epäonnistumiseksi (beta). Onnistumiset päivittyvät sitä mukaan malliin, kun niitä saadaan pyydykseen. Mandariinikokeen perusteella saimme alphaksi 20 ja betaksi 80. Alpha ja beta voidaan kuvitella pseudohavaintoina. Koska prioriin sisältyy reilusti epävarmuutta, käytimme alphan ja betan määrinä suhteellisia lukuja jotka olivat alkutietoja pienempiä, eli alpha 2 ja beta 8. Tämä kuvastaa epävarmuutta siitä, että kalat käyttäytyisivät samalla tavalla kuin mandariinit.
Pyydyksen malli alla:
# q = the effectiveness of the sampling device following a bete
# distribution with parameters alpha (=success) and beta (=failure)
q~dbeta(alpha,beta)
alpha<-2 # mandarines in the sampler, “less precise” (but with the #same ratio)
beta<-28 # mandariines elsewhere “less precise” (but with the same #ratio)
Kalojen määrää pyydyksessä päädyimme kuvaamaan ensin binomijakaumalla, koska kala joko on tai ei ole pyydyksessä. Populaation koko voi kuitenkin tällöin saada hetkellisesti x:ää pienempiä arvoja, joten teknisenä ratkaisuna käytimmekin poissonjakaumaa, jolloin kyseinen onglema ei häiritse mallia. Tähän asiaan kaipaisimme vielä lisäselvitystä. Q liittyy kiinteästi x:ään, kuten mallista huomaamme.
Pyydykseen päätyvien kalojen malli:
# x[i] = the daily catch (num. of fish caught at day i)
lambda[i] <- q*n[i]
x[i]~dpois(lambda[i])
Kalojen määrä pyydyksessä per päivä, tiistaihin 28.4.2015 asti.
list(m=60)
x[]
0
0
0
1
2
2
0
0
0
1
1
1
0
2
1
0
0
0
1
3
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
NA
END