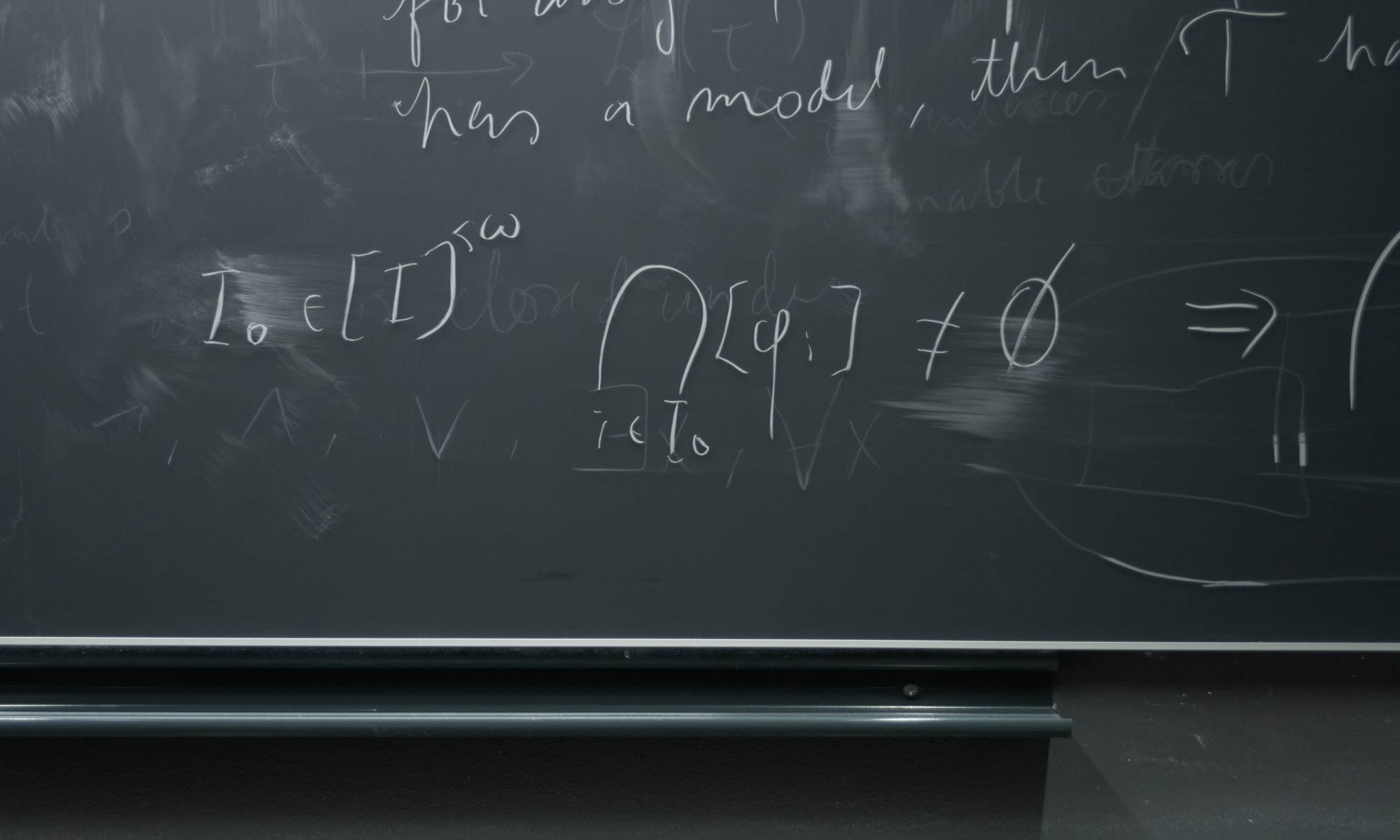The Autumn 2023 edition of the seminar was organized by Jonathan Pim and Julia Sanders.
| Autumn 2023 | Speaker |
|---|---|
| 8 September 2023 | Boxing and unboxing the black box of AI
Janne Siipola Neural networks are functions that have gained growing popularity in recent years. In this talk I will discuss about the basics of AI. We will begin with thinking what does one mean with the black box of AI and take a look at some of the recent applications. After that I show some of the efforts people have made to understand neural networks solutions within mathematical problems, especially within partial differential equations. Expected Length: 30-45 minutes Goal: Advertise neural networks, familiarize the audience to neural networks, give a glimpse into the mathematical theory on neural networks. Target audience: PhD students |
| 22 September 2023 | How to build a team
Matilda Häggblom In team semantics formulas are evaluated in a set of assignments, called a team, as opposed to a single assignment under the usual semantics. Team semantics allow us to examine various relationships between variables, such as dependence, independence, exclusion, and inclusion. Expected Length: 25-30 minutes. Goal: Explain in a simple way how to build teams to prove some implication problems for dependence atoms. Target audience: PhD and MSc students. |
| 6 October 2023 | Randomizing sums for fun and profit
Petri Laarne You can make some divergent sums converge just by randomly flipping the signs of the summands. The price to pay is that the convergence is only almost sure, but in exchange one gets almost unbelievably good probabilistic bounds. In this talk we’ll explore the proof and its ingredients, and also peek at some applications. Expected Length: 30 to 45 minutes. Goal: Showcase a nice result, and try to unravel the ideas behind a proof to a general audience. Target audience: Some knowledge of probability (e.g. Todennäköisyyslaskenta II) and analysis (L^p spaces) might make the talk more relevant, but is not strictly necessary. |
| 20 October 2023 | Quasiregularly elliptic closed Riemannian manifolds
Susanna Heikkilä We define the quasiregular ellipticity of a closed Riemannian manifold; the focus is on the intuitive idea and not on technical details. We also discuss examples of both quasiregularly elliptic and not quasiregularly elliptic closed Riemannian manifolds. Expected Length: 30 minutes. |
| 3 November 2023 | A Brief Introduction to Hyperfunctions
Sami Vihko What lies beyond Laurent Schwartz’s theory of distributions? In this talk, I aim to provide one possible answer to this question: Mikio Sato’s theory of hyperfunctions. Distributions and hyperfunctions are different classes of generalized functions, mathematical objects that have “function-like” qualities but do not strictly fit into the classical definition of a function of real or complex variables. While distributions are linear functionals from the space of test functions of real variables to the real numbers, hyperfunctions can be viewed as boundary values of complex analytic functions in some sense. Distributions can also be viewed as boundary values of analytic functions, but then there will be some growth conditions. Formally, if we remove these growth conditions, we obtain the hyperfunctions. In this talk, after the formal introduction, we will first take a brief look at the theory of distributions in an arbitrary dimension d. Towards the end of this part, we will restrict our discussion to the case of d = 1 and present a representation result for distributions to pave the way for hyperfunctions. Subsequently, we will define the space of hyperfunctions and present some properties of them. Finally, we will demonstrate that the theory of hyperfunctions encompasses the theory of distributions. We aim to keep the prerequisites to a minimum, but we do assume some background in complex/real analysis. At the very least, you should have a good understanding of what a complex/real analytic function is. While no knowledge of distribution theory is required, some familiarity with it is probably useful. Our objective is to provide a brief overview of this subject from an elementary point of view, so we will not present detailed proofs. Expected Length: 45 minutes. |
| 17 November 2023 | Concentration Inequalities: techniques for bounding rare events
Patrik Nummi In this talk, I will discuss concentration inequalities in probability theory. Broadly speaking, these are mathematical tools that seek to quantify how likely it is for a random variable to deviate from some number (e.g. its mean) by a certain amount. In addition to being interesting on their own right, these bounds are useful in many applied fields of stochastics, such as in Extreme value theory (quantifying probabilities of extremely rare events); Algorithmic analysis (proving bounds on the error probability of randomized algorithms); Statistical inference (providing bounds on the probability that an estimator deviates significantly from its true value); and Machine learning (providing bounds on the difference between empirical and expected risk). I will start with the well-known workhorses of real analysis, the Markov and the Chebyshev inequalities, and discuss how one can obtain further tail probability bounds from these elementary inequalities; in particular, we will consider sums of independent random variables, for which the Hoeffding and the Bernstein inequalities offer exponentially decaying bounds on the probability of deviations from expected values. I will also briefly discuss how these ideas can be generalised to higher dimensions (e.g. to Banach-valued random elements) and heavier-tailed distributions by introducing suitable Orlicz spaces, and their alternatives. Expected Length: 45 minutes. |
| 1 December 2023 | Issues and wrong conclusions in statistical testing
Lauri Tarpila Phrases like ”All models are wrong”, “This could all be just happening be in your head” or “We need assumptions for science to work” are common for someone who delves deep into science. In my presentation I am trying to clarify the origin of these phrases and explain it in a scientific way. My conclusion is that science could be understood as a tool for “unscientific” matters rather than as an objective and justified point of view on its own. This interpretation is, in my opinion, the most consistent with all the issues in the previously shown phrases and with scientific thinking. I will try to validate this by showing how, in my opinion, it is impossible to verify assumptions with statistical tests and unambiguous model selection is impossible. Expected Length: 30 minutes. |
| Postponed | Mathematical flexibility in university mathematics
Sara Parikka Mathematical flexibility refers to the combination of mathematical skills and understanding that allows for an optimal approach to solving equations. Flexibility is an essential aspect of a deeper understanding of strategies, their application, and the development of mathematical competence and thinking. The role of flexibility in mathematical proficiency has gained increasing attention in both research and teaching. Previous studies on flexibility have primarily focused on mental arithmetic and elementary algebra among middle school students. At the university level, mathematical flexibility has been examined in the context of differential calculus and basic computation. Knowledge about flexibility in different areas of mathematics remains limited, and research on flexibility in the context of university students is scarce, despite its crucial role in mathematical competence and learning. Expected Length: 30 minutes. |
The Spring 2023 edition of the seminar was organized by Petri Laarne and Susanna Heikkilä.
| Spring 2023 | Speaker |
|---|---|
| 20 January 2023 |
Jonathan Pim
Evading Epsilons with Ultrafilters Expected time: 20 or maybe 30 minutes. |
| 3 February 2023 |
Davide Quadrellaro
Szemeredi’s Regularity via Counting Measures Expected length: 45 minutes. |
| 17 February 2023 |
Heli Virtanen (double talk)
High school students and vectors: What kind of misconceptions arise? Expected length: 20 min. Summamutikka: Mathematics science class Expected length: 20 min. |
| 3 March 2023 |
Ensio Suonperä
Bilevel optimization with single-step inner method Expected length: 20 minutes (or little more) |
|
17 March 2023
Exceptionally in room Exactum B120. |
Siiri Kivimäki The notion of a logic, topologically There is way to associate a topological space to each abstract logic, in such a manner that important properties of the logic reflect as topological properties of the space. For instance, a logic is compact if and only if its corresponding space is compact. In this talk, I will discuss the notion of a logic, define its associated topological space, and sketch ways to obtain information of the logic by studying its corresponding space. The ultimate motivation comes from the fact that in first-order model theory, the most important tool is a topological one: the so-called space of types. I will try to start from the beginning and motivate everything through a lot of examples. Expected length: about 30 minutes |
| 31 March 2023 |
Joni Puljujärvi
A brief introduction to non-standard analysis In the 1690s, Leibniz and Newton developed calculus based on the notion of infinitesimally small quantities; e.g. the integral of a function f on an interval [a,b] is the (infinite) sum of the areas f(x)dx of infinitely thin rectangles, where x ranges over [a,b], f(x) is the height of the rectangle and dx, an infinitesimally small number, is the base of the rectangle. However, the notion of infinitesimals was ultimately deemed non-rigorous and was replaced as the basis of calculus by the epsilon-delta definition of a limit, due to Weierstrass in the 1870s. This mindset of epsilons and inequalities, as opposed to infinitely small distances, is still the basis of today’s analysis. However, Robinson in 1960 discovered a way to treat infinitesimals with the rigor of modern mathematics which lead to the birth of the field of non-standard analysis. In this talk, I will briefly describe the framework of hyperreal numbers and how infinitesimals can be used to give the basic definitions of calculus, following the intuition of Leibniz and Newton but with the rigor that is acceptable to a modern mathematician. Expected length: 45 minutes |
|
4 April 2023 (Tuesday)
Exceptional date; room Exactum CK111. |
Tapio Saarinen
The categoricity of theories in second-order logic Mathematicians are often interested in characterising various objects by describing what axioms they satisfy. A theory (think: a list of axioms) is categorical if it has only one model up to isomorphism: thus the theory completely characterises the model. Any finite structure can be finitely axiomatized with first-order logic, but if a first-order theory has an infinite model it will be non-categorical. Conversely, many natural structures (such as the real numbers as a complete ordered field) have categorical second-order axiomatizations. Therefore one may wonder how often this happens: are most second-order theories categorical? The answer to this question, in most cases, turns out to be independent of the axioms of set theory. I will define second-order logic, motivate the question and (hand-wavingly) define and discuss various set-theoretic assumptions that have implications on the matter of second-order categoricity. Expected length: 30 minutes |
| 21 April 2023 |
Julia Sanders
Numerical Solution of a Schrodinger Bridge Problem using Forward-Backward Iteration The Schrodinger bridge problem was originally posed in 1931 and since then has found many applications. Here, we fix initial and final probability distributions and find a stochastic process that satisfies these while minimising a cost function (e.g. the Kullback-Leibler divergence) between a reference process. The problem can be rephrased as a system of partial differential equations (PDEs), which, in a particular case, simplify to two linear PDEs with coupled boundary conditions. I will describe an algorithm for computing a numerical solution for this type of problem that uses a forward-backward iterative procedure. Expected length: 30 minutes |
| 5 May 2023 |
Aapo Laukkarinen
Sparse domination and weighted norm inequalities Sparse domination is a recent technique in harmonic analysis that allows one to dominate various complicated operators by sums of averages taken over cubes that have “large” disjoint subsets. This type of domination is primarily motivated by the sharp quantitative weighted norm inequalities that arise from it. In this talk I will introduce the fundamental definitions related to sparse domination and discuss some sparse domination results and weighted norm inequalities that follow. Expected length: 30-45 minutes perhaps |
The Autumn 2022 edition of the seminar was organized by Jaakko Sinko and Aleksis Vuoksenmaa.
| Autumn 2022 | Speaker |
|---|---|
| September 2nd 2022 |
Susanna Heikkilä Differential forms in Euclidean spaces In this talk, we will discuss the basics of differential forms. In particular, we will only work with differential forms in Euclidean spaces and manifolds will not appear in the talk. Differential forms in Euclidean spaces provide an alternative, more general, approach to multivariable calculus. We will begin by presenting necessary preliminaries in multilinear algebra. After introducing the definition of differential forms, we will study the exterior derivative. For the remainder of the talk, we will consider closed and exact differential forms. We will also cover multiple examples throughout the talk. The talk is intended for anyone interested in expanding their general knowledge in mathematics. Thus, the talk is aimed at a broad audience and elementary knowledge of linear algebra and vector analysis is sufficient for attending the talk. Presentation slides: differential_forms_domast |
| September 16th 2022 | Otto Rajala
Forcing and the continuum hypothesis – how to prove that we cannot prove I will present the main ideas of set theoretical forcing and sketch a proof showing that the continuum hypothesis cannot be proven true or false from the axioms of set theory. The most famous result in the history of set theory is the proof that the continuum hypothesis (CH) cannot be proven true or false from the usual axioms of set theory. CH claims that there is no set that is larger than the set of natural numbers but still strictly smaller than the set of real numbers. Forcing is the main technique used to construct models that show that the axioms do not prove or disprove a given statement. It was first developed specifically to prove the independence of CH. I will start by introducing the basics of set theory and define ordinals and cardinals and then continue to present the basic ideas of forcing. I will then sketch how we can apply forcing to show the independence of CH by building a model where CH does not hold and another model where CH is true. If time permits, I will briefly present my own work. The talk does not presuppose any background knowledge in set theory or logic. I try to present the ideas in an intuitive and untechnical manner, so that the talk can be interesting to any mathematician who would like to know a bit more about set theory. |
| September 30th 2022 | Max Sandström
What Does Time Have to Do with Logic?: a Brief History of Logic, Time and Computation In this talk I aim to give a conceptual and historical background to my research, in order to give perspective on the field of temporal logic and its applications in computer science. I will take you on a sightseeing tour across millennia, showing how considerations of time have played a part in the development of logic, how the emergence of digital computers gave these considerations a renewed focus, and how formal approaches to the study of dependence can plot a course for the field into the future. The talk will not be technical at all and is suitable for a general audience regardless of background or experience with logic. |
| October 14th 2022 | Patrik Nummi
Multiple Stochastic Integration and Homogenous Chaos In this talk, I will give a brief introduction to the theory of stochastic integration with respect the Brownian motion process, with a particular focus on multiple integration. I will then move to a slightly more abstract Hilbert space setting to introduce the concept of homogenous chaos, or Wiener polynomial chaos, dealing with representing L^2-random variables in terms of polynomial functions of Gaussian random variables. Finally, the aim of the talk will be to introduce the Wiener-Itô theorem, which states a fundamental connection between multiple stochastic integrals and the orthogonal decomposition of L^2 given by homogenous chaos. The talk is given from a real / functional analysis point of view, and is intended for anyone interested in obtaining some rudimentary knowledge about stochastic integration and its connection to Hilbert space theory. Thus minimal prior knowledge of stochastics is required. Presentation slides: patrik_nummi_DOMAST_presentation |
| October 28th 2022 | Ilaria Pia
An introduction on statistical model comparison and selection: objectives, methods and applications
Statistics is a science based on data. When implementing a statistical model using reliable and unbiased data as well as defining the objective of our model is crucial. Furthermore, to select a good model, we need to be able to properly evaluate its performance. In this talk I will introduce statistical model selection methods, while addressing the following questions: what are the main steps to follow when implementing a statistical model and how do we select a good model? After a brief introduction about statistical models and their principal objectives, I will present an overview of the most popular techniques in model selection, taking a decision theory point of view, with a focus on Bayesian statistics. I will conclude with some applied example in ecological statistics. The talk is targeted to anyone interested in gaining some knowledge about statistical model selection, from a general perspective. Not much technical terminology is involved, and no previous statistical knowledge is required. |
| November 11th 2022 | Antti Aro
Renormalization Group approach to Stochastic Quantization In this talk I explain the ideas behind using Renormalization Group to study physical systems at different scales and the use of Stochastic Quantization to study quantum mechanics through the use of stochastic partial differential equations. I will also give the broader historical context and justification for these concepts. Finally these ideas are combined into a simple calculation aimed at understanding quantum mechanics on arbitrarily small scales. The talk is aimed at a broad audience with general knowledge of mathematics and physics. The goal of the talk is to explain what Renormalization Group and Stochastic Quantization are, their broader historical context and how they look in an actual calculation. Presentation slides: RGSQpresentation |
| November 25th 2022 | Elli Karvonen
Inverse problem meets computational topology In this talk, I will present the main ideas of my current research, which combines inverse problems and computational topology, namely limited angle tomography and persistent homology. Limited angle tomography is an X-ray imaging technique that allows one to study the interior structures of an object. It results in a much harder reconstruction problem than a full-angle case. Despite an algorithm, certain parts of the object’s boundaries cannot be detected stably in limited angle cases. This means parts of the boundaries are missing. We aim to estimate the missing parts with the help of persistent homology. Persistent homology is a computational tool to measure topological features of the data, i.e., different dimensional holes. Since the boundaries of the object form loops, we can implement homology to detect does estimated boundaries’ parts occur together with known boundaries. The talk does not presuppose any background knowledge of inverse problems or homology. The content of the talk is not highly technical and should be accessible to a broad audience. |
| December 9th 2022 | Jonas Lindblad
Exponential functionals of stochastic processes with applications The study of exponential functionals of Brownian motion emerged from the physics literature via the desire to characterize the partition function of certain models of disordered systems. At the same time the exponential functional of a Brownian motion with drift was investigated as the time-average of a risky asset in the Black-Scholes framework of mathematical finance – as such it is a quantity used in pricing Asian options. Finally, the exponential functional of a stochastic process has an obvious interpretation as a discounted cash flow and consequently is a model of random growth or decay. This talk introduces exponential functionals of stochastic processes (in particular Lévy processes) and what can be said about their distributional properties by providing a historical overview of related problems in physics and finance. To this end, the explicit distribution for certain special cases is derived, while moment formulas are studied for a more general class of functionals. For infinite functionals the celebrated Dufresne identity, which characterizes the Gamma distribution as the reciprocal of the integral of Geometric Brownian motion, is proven. The talk does not assume a strong background in probability or any of the mentioned research areas. It is largely self-contained and, although familiarity with probability obviously helps, is aimed at a relatively elementary level that advanced undergraduates are likely to find suitable. Presentation slides: rand-exp |
The Spring 2022 edition was organized by Patrik Nummi.
| Spring 2022 | Speaker |
|---|---|
| 21 January 2022 |
Jaakko Sinko A necessary condition for compactness of commutators of singular integrals We study commutators [b,T]=bTf-b(Tf) from L^p to L^p, that are associated to a Calderón-Zygmund operator T and a function b. The condition that b is a VMO function is necessary for the compactness of such a commutator. We extend an earlier result of Lacey & Li to a larger class of Calderón-Zygmund kernels and also to complex-valued multiplier functions b. Through this result, the aim is to give some insight into my research. Prerequisites: At least, a basic understanding of L^p spaces is needed. |
| 4 February 2022 | Susanna Heikkilä
Geometry of quasiregular mappings and curves In this talk, I will discuss quasiregular mappings and curves. I will go through both definitions and give geometric interpretations for them. I will also present multiple examples and briefly mention some results. This talk is aimed at a broad audience and the goal is to focus on introducing the concepts of quasiregular mappings and curves. Presentation slides: qr_maps_and_curves |
| 25 February 2022 | Janne Siipola
Ritz method meets neural nets In this domast seminar talk we turn from the highway of variational calculus to the path which starts in the Ritz method and ends, at the moment, to Deep Ritz method. In the talk I shortly present the original Ritz method and how it influenced the finite elements method and the Deep Ritz method, which is the latest computational method in this line of research. Goal of this talk is presented above; present those connections to the audience. I try to skip the heavy details and proofs and focus on the main ideas as clearly as possible. |
| 11 March 2022 | Patrik Nummi
Fractional Gaussian fields and the multiplicative chaos measure In this talk, I will introduce fractional Gaussian fields and the so-called multiplicative chaos measure induced by such fields. I will discuss the ways to construct these mathematical objects and present some of their key properties. The talk is intended for anyone interested in obtaining some rudimentary knowledge about Gaussian random generalised functions from a real analysis perspective, and minimal prior knowledge of stochastics is required. Presentation slides: fractional_gaussians_and_GMC_slides |
| 25 March 2022
|
Joni Puljujärvi
Using games for measuring similarity between mathematical structures We give a brief introduction to the so called Ehrenfeucth–Fraïssé games and how they can be used to determine whether two mathematical structures look similar in the eyes of logic. We also discuss some recent developments in metric variants of the games. Presentation slides: Domast_Student_Seminar_2022 |
| 8 April 2022 | Saara Sarsa
On the regularity theory of p-harmonic functions For 1<p<\infty, p-harmonic functions are minimizers of the p-energy functional and solutions to a degenerate/singular elliptic PDE. A well-known example are 2-harmonic functions (harmonic functions in short) that minimize the classical Dirichlet energy. In this talk I discuss on the classical regularity theory of p-harmonic functions. First I will give a short introduction to the questions and ideas in elliptic regularity theory in general. After that, my main goal is to explain some ideas behind the proof that gradient of a p-harmonic function is Hölder continuous.
|
| 29 April 2022 | Marcus Rosenberg
Floquet transform and its applications to PDEs We present the basics of Floquet transform in periodic domains. We then show some nice results for elliptic and or parabolic PDEs in periodic domains. |
| 6 May 2022 | Petri Laarne
Invariant measures: what and why Invariant measures arise in statistical mechanics. We illustrate their definition and properties on finite-dimensional spaces, and then move on to PDEs. We take a nonlinear Schrödinger equation on 1D torus as our example, and see how a random Fourier series yields an invariant measure. As the result, we get improved regularity theory of “almost all” solutions. I assume that the audience has heard of differential equations, L^p spaces, and Fourier transform — but willingness to accept what I claim about them is enough. I will skip technicalities liberally, and each tool is independent of the others. The talk roughly follows my MSc thesis. Presentation slides: Laarne_Domast_invariant_handout |
| 13 May 2022 | Kalle Koskinen
Basic structure and methods of proof for random probability measures Random probability measures serve as an interesting example of metric space-valued random variables. In this presentation, we will give a high-level overview of some basic methods of proof concerning uniform tightness, weak convergence, and the distributions of random probability measures. Our hope is that by the end of the presentation, the audience will appreciate the notions of expectations of expectations and distributions of distributions in the context of random probability measures. Presentation slides: random_measures |
| Autumn 2021 | Speaker |
|---|---|
| 3 September 2021 |
Olli Hirviniemi Quasiconformality, distortion and regularity: an introduction The notion of quasiconformality is nearly a century old yet still provides some interesting research questions. We first discuss the concept of quasiconformal mappings and more general mappings of finite distortion. Then we study both old and new regularity results in this setting. Both geometric and analytic regularity are considered, with the aim of presenting the research to broader audience. |
| 17 September 2021 | Saara Sarsa
Insights into the regularity theory of elliptic partial differential equations: from Hilbert’s 19th problem to the 21st century In 1900, in the International Congress of Mathematics, David Hilbert presented his famous collection of problems. The problems of Hilbert have inspired mathematicians throughout 20th century, and up to today.
Hilbert’s 19th problem is: Are the solutions of regular problems in the calculus of variations always necessarily analytic?
In my talk, I will
(a) explain the Hilbert’s 19th problem,
(b) present the way it was solved, focusing on ideas rather than rigorous proofs; and
(c) discuss my own research on the regularity theory of elliptic partial differential equations, and how it connects to the Hilbert’s 19th problem.
The goal of my talk is to provide historical perspective to the modern research of regularity theory of elliptic partial differential equations. The talk is aimed at a broad audience. No deep understanding of the topic is expected and all Domast students from any subfields of mathematics are warmly welcome.
|
| 1 October 2021 | Tommi Heikkilä
4D Dual-tree complex wavelet transform for time dependent data Regularization is the key to solving ill-posed inverse problems, such as computing tomographic reconstructions from noisy and limited data, and sparsifying representation systems such as wavelets are a common and reliable choice. If we consider repeated cone-beam measurements of a dynamic object of interest, the regularized object is 4-dimensional (3D + time)! Motivated by this challenge we extend the dual-tree complex wavelet transform to 4D and apply it to sparse dynamic tomography regularization. The aim is to give a rough idea on the construction of the 4D dual-tree complex wavelets, how the implementation can be made relatively simple and briefly illustrate what are the advantages of using complex valued wavelets over traditional real valued ones. Finally we compate both in 4D sparse dynamic tomography setting. |
| 15 October 2021 | Riku Laine
Evaluating Decision Makers over Selectively Labelled Data: A Causal Modelling Approach We present a Bayesian approach to evaluate AI decision systems using data from past decisions. Our approach addresses two challenges that are typically encountered in such settings and prevent a direct evaluation. First, the data may not have included all factors that affected past decisions. And second, past decisions may have led to unobserved outcomes. This is the case, for example, when a bank decides whether a customer should be granted a loan, and the outcome of interest is whether the customer will repay the loan. In this case, the data includes the outcome (if loan was repaid or not) only for customers who were granted the loan, but not for those who were not. To address these challenges, we formalize the decision making process with a causal model, considering also unobserved features. Based on this model, we compute counterfactuals to impute missing outcomes, which in turn allows us to produce accurate evaluations. As we demonstrate over real and synthetic data, our approach estimates the quality of decisions more accurately and robustly compared to previous methods. |
| 22 October 2021
(moved to take place one week earlier due to AGENT) |
Eugenia Franco
Coagulation equation with source
Smoluchowski’s coagulation equation describes the evolution in time of a system of atmospherical particles, coagulating upon binary collision.
It is the aim of this talk to present the main features of the Smoluchowski’s coagulation equation and to introduce one of its possible generalization: the coagulation equation with a source term.
The asymptotic behaviour of the solutions of this equation is not known for the coagulation kernels relevant for atmospheric science applications. I will conclude the talk by presenting a conjectured behaviour.
|
| 12 November | Emil Airta
Commutator bounds using paraproducts and duality estimates Representation theorems have been one of the most influential tools in the modern studies of singular integrals. Via dyadic-probabilistic methods, we may reduce our study from complicated singular integrals to simpler dyadic model operators. For the model operators, it is much easier to study boundedness in various settings. Some applications include the commutator results.
This presentation aims to present an upper bound proof of a commutator with the simplest model operator. We will recall some results from the basic courses of Real and Harmonic analysis. Hence, no preliminary knowledge is required.
|
| 3 December
(postponed by one week due to DOMAST day, the new date is visible) |
Aleksis Vuoksenmaa
Wick polynomials and their application in the kinetic theory of the Discrete Nonlinear Schrödinger equation (DNLS) Wick polynomials (also known as Wick products or Wick monomials) are linear combinations of random variables that satisfy nice additional properties that make them useful in the study of the time evolution cumulants of random variables. In this talk, I will give a basic overview of Wick polynomials and cumulants, some of their properties, as well as different ways of defining them. Time permitting, I will discuss how Wick polynomials can be used in the study of the kinetic theory of the Discrete Nonlinear Schrödinger equation.
|
| 10 December | Ekaterina Mukooseva
Free Boundary Problems: An introduction In this colloquium-style talk I will tell you about state-of-the-art in free boundary regularity. We will see what problems there are in the field, what methods are used to deal with them and what remains unsolved. No prerequisites, although standard PDE regularity knowledge wouldn’t hurt. |
| 17 December | TBA |
| Spring 2021 | Speaker |
|---|---|
| 22 January 2021 |
Jorma Kilpi
Statistical analysis of data that has heavy-tailed characteristics |
| 5 February 2021 | Anna Suomenrinne-Nordvik Mathematical and practical challenges in modeling COVID-19 Use of mathematical modeling to understand infectious disease dynamics as well as predicting future outcomes has played a significant role in management of the current pandemic. The coronavirus modeling group at the Finnish institute of health and welfare uses an age-structured SEIR model, and while this model is well studied, determining model parameters is an ill-posed inverse problem. The novelty of the virus also presents issues as there is on one hand poor prior knowledge and on the other hand an extensive amount of new research published in recent months. Rapid changes in the population contact structure due to restrictions and individuals adapting their behavior pose additional challenges. In this talk I will present parts of the coronavirus modeling work done at the Finnish institute of health and welfare as well as some mathematical and practical challenges in the work. |
| 19 February 2021 | Riina Virta Gamma emission tomography of spent nuclear fuel Disposal of spent nuclear fuel is a timely topic in Finland, where a geological repository for such disposal is currently being built. Before the spent nuclear fuel can be buried in the bedrock, the contents of the fuel need to be verified to avoid possible diversion of nuclear material. For this safeguards purpose, a non-destructive assay method Passive Gamma Emission Tomography (PGET) is used. With the help of modern inverse computing, a cross-sectional image of the fuel can be reconstructed. Both the attenuation and activity of the spent fuel can be seen and even a single missing fuel rod can be detected. |
| 5 March 2021 | Antti Mikkonen Radiative transfer in atmospheric remote sensing Remote sensing of atmospheric constituents vastly expands the available data compared to in situ measurements. One atmospheric remote sensing method is measuring the scattered and reflected solar radiation using satellite-based spectrometers. Determining the state of the atmosphere from a radiation spectrum is an ill-posed inverse problem. The full retrieval process of atmospheric carbon dioxide will be examined with the focus on the forward modeling. In general case, the forward model is the radiative transfer equation (RTE), but in practical situations numerical methods and approximations are necessary. Two radiative transfer simulators, Siro and RaySca, will be presented. |
| 19 March 2021 | Tuomas Oikari Singular integrals and applications We outline some motivating examples from partial differential equations and rectifiability of sets for the study of singular integral operators and their commutators. The boundedness theory for both classes of operators is also discussed. |
| 26 March 2021 | Mikko Heikkilä Differentially private partitioned variational inference Variational inference is a common method in Bayesian learning for approximating intractable posterior distributions. Partitioned variational inference (PVI) is a recent formulation that unifies many previous variational inference algorithms within a single framework. PVI is especially well suited for federated learning scenarios, where the data are distributed over many participants. In this talk I will discuss our work on combining PVI with differential privacy, a strict mathematical definition of privacy, to enable learning variational approximations in the federated setting while guaranteeing privacy for the individual data subjects. |
| 9 April 2021 | Joona Oikarinen On the Origin of Spin The aim of this presentation is to explain how spin appears in Quantum Mechanics when implementing rotational symmetry. On the mathematical side this leads us to study projective representations of symmetry groups on projective Hilbert spaces and their lifts to the universal cover of the group. Then we study how the projective representation on the universal group can be lifted to a unitary representation on the Hilbert space. On the physical side we study how the mathematics leads to the appearance of the spin observables for the electron. |
| 16 April 2021 | Stefanos Lappas Extrapolation of compactness on weighted spaces The extrapolation theorem of Rubio de Francia is one of the most powerful tools in the theory of weighted norm inequalities: it allows one to deduce an inequality (often but not necessarily: the bounded of an operator) on all weighted L^p spaces with a range of p, by checking it just for one exponent p (but all relevant weights). My topic is an analogous method for extrapolation of compactness. In a relatively soft way, it recovers several recent results about compactness of operators on weighted spaces and also gives some new ones. |
| 30 April 2021 | TBA |
| Fall 2020 | Speaker |
|---|---|
| 4 September 2020 | Eugenia Franco One dimensional reduction of a Renewal Equation with a continuum of states at birth Structured population models aim at studying phenomena at the population level, starting from mechanisms at the individual level. Individuals are characterized by their state (age, size, immunity level, …) and appear (for example through birth) in the population with a certain state, which is called state at birth.
If the set of the states at birth is finite it is possible to formulate the model as a Renewal Equation; the asymptotic behviour of its solution can be studied with the Renewal Theorem.
When, instead, we deal with a continuum of states at birth we can still easily formulate the model as a Renewal Equation, but its analysis will typically be difficult.
The focus of this talk is on the second case and on linear Renewal Equations.
Since a Renewal Equation is an integral equation it is chracterized by an integral kernel, which is the bridge between the mathematical formalization and the biological interpretation.
In the first part of the talk I will focus on the modelling aspect, presenting also some examples.
In the second part of the talk I will explain how, under a factorization assumption on this kernel, it is possible to deduce the asymptotic behviour of the solution of the Renewal Equation.
|
| 18 September 2020 | Akseli Haarala On the electrostatic Born-Infeld equations and the Lorentz mean curvature operator In 1930’s Born and Infeld proposed a new model of nonlinear electrodynamics. In the electrostatic case the Born-Infeld equations lead to the study of a certain quasilinear, non-uniformly elliptic operator that comes with a natural gradient constraint. The same operator appears also as the mean curvature operator of spacelike surfaces in the Lorentz-Minkowski space, the setting of special relativity. We will explain both of these contexts to motivate the mathematical study of said operator.Our main focus will be on the regularity of the solutions of the electrostatic Born-Infeld equations. We will talk about some now classical results as well as some recent developments. We hope to give some ideas on the problems and methods involved without going into details. |
| 2 October 2020 | Tommi Heikkilä Shearlet regularization in applied dynamic tomography Tomography is a common example of an ill-posed inverse problem where in order to gain information on the object of interest, the incomplete, indirect and noisy measurements need to be complemented with additional information. This process is known as regularization and a wide variety of options have been developed over the years. In particular wavelets and their extensions are a robust choice in many situations. The aim of this talk is to give a brief introduction to tomography and motivate the regularization process using shearlets – which are quite a modern representation system for multivariate data such as images or animations. |
| 16 October 2020 | Kalle Koskinen Convergence of local observables in a statistical ensemble model of a simple paramagnet In physics literature, ensemble equivalence is usually evoked to swap between less computationally tractable models to more computationally tractable models. Although ensemble equivalence is effectively a very elaborate parameter matching scheme, it is then tacitly assumed that any relevant information of the model is carried over. In this presentation, we will go through the basics of ensemble equivalence and apply these results to prove convergence of local observables between two distinct statistical ensemble models of a simple paramagnet. In doing so, we will have given a completely rigorous example of the interchange between statistical ensembles at the level of local observables. |
| 30 October 2020 | Brecht Donvil (Time exceptionally 13-15) A short introduction to open quantum systems The goal of open quantum systems is to study the impact of the environment on the dynamics of a quantum system. The study of such systems today is perhaps more relevant than ever due to the development of genuine quantum devices such as quantum computers. Generally it can be said that the influence of the environment is detrimental to the working of these devices. In my talk I will focus on one of the simplest examples of an open quantum system: a qubit, i.e. a quantum bit, in contact with a thermal environment. Using this example I will sketch the scene of open quantum systems and present some of the main results. Finally, I will tie this in with some results I derived working on my PhD. |
| 13 November 2020 | Emil Airta Introduction to singular integrals and commutators In the field of harmonic analysis, the most central objects are the singular integrals. One of the most studied ones are the Calderón-Zygmund operators; the history of classical studies dates to the mid-1900s. Recently, commutator estimates of these operators have drawn more attention. In this talk, I aim to present some reasons for this.The focus of the talk is to introduce the most basic examples of singular integrals and the related commutator estimates. Moreover, we briefly consider singular integrals on a general form and present some classical questions. |
| 27 November 2020 | Stefanos Lappas The dyadic representation theorem using smooth wavelets with compact support The representation of a general Calderón–Zygmund operator in terms of dyadic Haar shift operators first appeared as a tool to prove the $A_2$ theorem, and it has found a number of other applications. In this talk we present a new dyadic representation theorem by using smooth compactly supported wavelets in place of Haar functions. A key advantage of this is that we achieve a faster decay of the expansion when the kernel of the general Calderón–Zygmund operator has additional smoothness. |
| 11 December 2020 | Tuomo Nieminen Estimation of the time-dependent ratio of SARS-CoV-2 infections to registered disease cases, during the first wave of the 2020 COVID-19 outbreak in Helsinki and Uusimaa region, FinlandIn Finland, the first wave of a COVID-19 epidemic, the illness caused by new severe acute respiratory syndrom coronavirus 2 (SARS-CoV-2), occurred during the spring of 2020, with most of the disease cases in the extended capital region of Helsinki and Uusimaa (HUS area). The clinical manifestations of a SARS-CoV-2 infection ranges from asymptotic to severe, potentially fatal disease. The likelihood of a SARS-CoV-2 infection being registered as a disease case depends on the clinical manifestation as well as the testing policy and capacity at the time, which may miss mild and asymptomatic cases. COVID-19 disease cases are registered in the Finnish National Infectious Diseases Register (FNIDR). A large proportion of the infections were likely not registered as cases during the first wave of the epidemic in Finland due to testing policy and capacity as well as infections not developing into disease cases. Quantifying the relative difference in the numbers of registered cases and true infections is important, as assessing the severity of the disease caused by SARS-CoV-2 requires knowledge of the number of infections occurring in the population. Infections usually leave a mark in the form of antibodies, and so knowledge of the number of infections can be attained from serology studies. A population serology survey by the Finnish Institute for Health and Welfare (THL) obtains information on how large a proportion of the population have developed antibodies to SARS-CoV-2 in different regions in Finland (serology survey). The serology survey targets most areas in Finland and individuals aged 18-69. It is not straightforward to compare the results of the serology survey to the registered cases. The two sources of observations are not directly comparable during any time point as there may be a significant delay from the disease onset date to developing antibodies. To solve this issue, we utilise previously published information of the time to develop antibodies to project the population proportion of infected individuals with antibodies (i.e those who have seroconverted), when the registered infections in the FNIDR are the only infections. We compare the projections to the proportion of seroconverted observed in the serology survey and estimate the time-dependent ratio of infections to registered cases.
|