Tekijät: Miia Liimatainen, Milja Niemi, Saara Lehto & Venla Väli-Torola

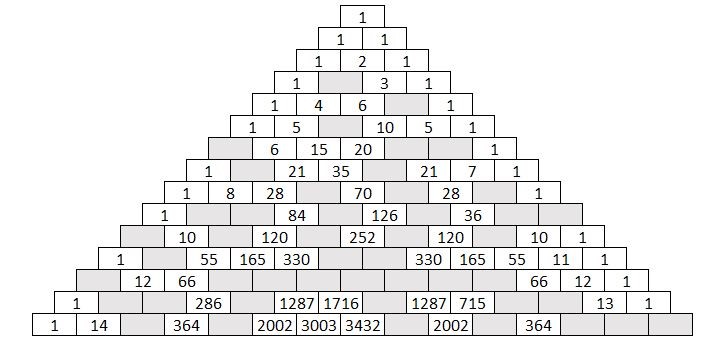
Tehtävänä on täydentää alla oleva pyramidi täyttämällä kaikki harmaat solut. Pyramidi lasketaan summaamalla jokaisen solun yläpuolella olevat kaksi solua. Halutessasi voit jatkaa pyramidia myös mallista alaspäin. Tätä pyramidia kutsutaan Pascalin kolmioksi.

Jos pyramidin tulostaminen ei onnistu, piirrä kolmio ruutupaperille kuten kuvassa. Täydennä tämän kuvan tummennettuihin soluihin oikeat summat. Jos haluat varmistua, että koko kuvio mahtuu paperille, aseta paperi vaakasuuntaan ja aloita aivan paperin ylälaidasta ihan keskeltä.

Kun olet valmis, väritä täydennetystä pyramidista kaikki viidellä jaolliset solut. Mitä huomaat?

Värien yhteenlasku

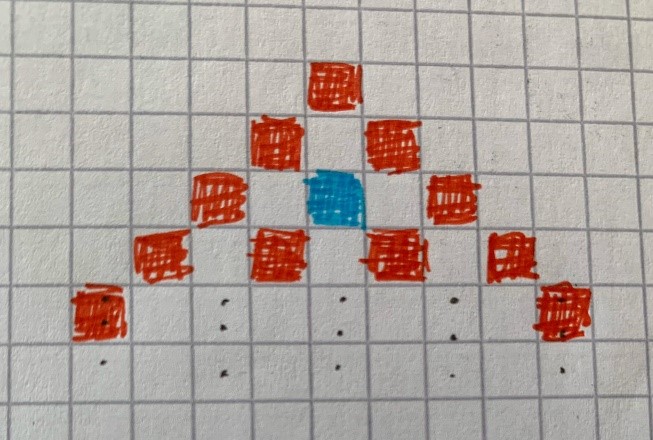
Väritä seuraavaksi samankaltainen kolmio värien yhteenlaskun avulla, seuraavien ohjeiden mukaan:

• Kolmion kärki ja sivut on väritetty punaisiksi
• Kahden punaisen solun tulos on sininen
• Kahden sinisen solun tulos on sininen
• Sinisen ja punaisen tai punaisen ja sinisen solun tulos on punainen

Aloita siis tähän tyyliin ja jatka alaspäin:

Voit myös vaihtaa värejä, mutta pidä huolta, että säilytät laskusäännöt. Korvaa siis säännöissä kaikki punaiset esimerkiksi keltaisella ja kaikki siniset esimerkiksi vihreällä.

Täydennä nämä väritykset numeroituun Pascalin kolmioon tai vertaa saatua kolmiota Pascalin kolmioon. Mitä huomaat? Osaatko selittää mitä värien laskusäännöt kuvaavat? Millaisia lukuja punainen väri vastaa? Millaisia sininen?

Miten kuvio jatkuisi alaspäin siitä mihin jäit? Voisiko väritystyötä helpottaa käyttämällä hyväksi kuvion toistuvuutta tai symmetrisyyttä?

Lopuksi

Googlaa Sierpinskin kolmio (Sierpinski triangle). Mitä yhtäläisyyksiä huomaat meidän pyramidiemme kanssa? Tee Googlen kuvahaku Sierpinskin kolmiosta. Mikä kuvista on oma suosikkisi?

Lisätehtävä: Millaisia kuvioita pyramidiin muodostuu, jos väritätkin kaikki kolmella tai neljällä jaolliset solut?

Täältä löydät tehtävien vastaukset!

Lisää Pascalin kolmion ihmeitä voit tutkia Mathigonin sivuilla: https://mathigon.org/course/sequences/pascals-triangle

Sierpinskin kolmio on fraktaalikuvio. Toisenlaiseen fraktaaliin voit tutustua Summamutikan materiaalipankin tehtävässä ”Kochin lumihiutale”: https://blogs.helsinki.fi/summamutikka/kochin-lumihiutale/