Teksti: Tinja Seppälä

”Hanoin tornin mysteeri väitetään pohjautuneen legendaan Hindutemppelistä, jossa palapelejä käytettiin nuorten pappien kurinalaisuuden parantamiseksi. Legendassa papeille annettiin 64 kultalevyä, jotka olivat pinottu siististi yhteen pylvääseen kolmesta. Jokainen levy lepäsi hieman suuremman levyn päällä. Pappien tavoitteena oli luoda pino uudelleen eri pylvääseen siirtämällä levyjä yksi kerrallaan toiseen pylvääseen niin, että isompaa levyä ei koskaan voitu sijoittaa pienemmän levyn päälle. Vaikka papit olivat tehokkaita ja siirsivät levyjä tahdilla yksi per sekunti, niin työn suorittamiseen olisi mennyt silti melkein 585 miljardia vuotta – yli 40 kertaa maailmankaikkeuden iän verran! Matematiikan avulla voidaan löytää tehokkain ratkaisu Hanoin tornin ratkaisemiseksi, ja tämän säännön keksi ranskalainen matemaatikko Édouard Lucas 1800-luvulla.”

HANOIN TORNIN RATKAISUEHDOTUS

Hanoin torni voidaan kuulemma ratkaista matematiikan avulla, vau! Mutta miten? Tutkitaan tätä…

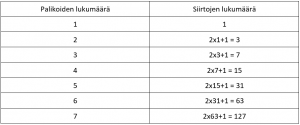
Millä tahansa määrällä levyjä voidaan teoriassa (käytännössä suurilla levymäärillä ratkaisuun saattaa mennä toivottoman paljon aikaa) ratkaista Hanoin torni, mutta vähimmäismäärä levyjä Hanoin tornin palapelin ratkaisemiseksi on 2n-1, missä n on levyjen lukumäärä. Taulukko levyjen ja siirtojen lukumäärän yhteydestä löytyy alempaa.

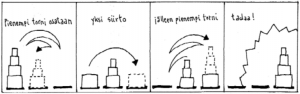
Hanoin tornin yksinkertainen eli iteratiivinen ratkaisu on se, että vaihdetaan vuorotellen pienimmän ja ei-pienimmän levyn paikkaa. Toisin sanoen, kun siirretään pienintä levyä, niin siirretään se aina seuraavaan kohtaan samansuuntaisesti (oikealle, jos kappaleiden aloitusmäärä on parillinen, ja vasemmalle, jos kappaleiden aloitusmäärä on pariton.) Esimerkiksi, jos aloitat kolmella levyllä, siirrä pienin levy vastakkaiseen päähän ja jatka sitten sen jälkeen toiseen suuntaan. Muitakin ratkaisukeinoja on olemassa, mutta yksinkertaistettuna voidaan käyttää tätä algoritmia ratkaisuun. (ks. yllä olevat kuvat ratkaisun hahmottamiseksi)

HANOIN TORNIN TARKASTELUEHDOTUS OPPILAIDEN KANSSA

Tutkivan oppimisen ja ilmiöpohjaisuuden lähtökohtina ovat todelliset maailmanilmiöt, joita tarkastellaan sellaisinaan aidossa kontekstissa. Tutkiva oppiminen ei ole pelkästään menetelmä, vaan ajattelutapa, jossa oppiminen tähtää ymmärtämiseen sekä ilmiöiden selittämiseen. Oppimisprosessissa lähdetään liikkeelle ongelmanratkaisun näkökulmasta eli tietoisen pohtimisen kautta. Oppilasta voidaan ohjata kohdistamaan huomiota keskeisiin käsitteisiin ja perustaviin ideoihin, mutta perusideana on, että oppiminen ja oivaltaminen lähtee oppilaasta itsestään.

Hanoin tornia voidaan lähteä tarkastelemaan niin, että joko digitaalisten työkalujen tai konkreettisen Hanoin tornia muistuttavan rakennelman avulla tarjotaan ensin oppilaille mahdollisuus tarkastella palapeliä pienissä ryhmissä omaan tahtiin. Pikkuhiljaa sääntöjä voidaan lisätä tarkastelun lisäksi ja tueksi, jonka jälkeen oppilaat voivat alkaa keksiä säännönmukaisuuksia, joilla Hanoin tornin palapeli voitaisiin kenties ratkaista. Nopeimmat voivat alkaa myös miettiä sitä, että kuinka monta siirtoa on minimimäärä tietyillä levymäärillä. Tässä käytettäisiin lähtökohtana tutkivaa oppimista, joka muun muassa kehittää oppilaiden ongelmanratkaisutaitoja ja saattaa lisätä mielenkiintoa tarkasteltavaa aihetta tai teemaa kohtaan. Kuitenkin lopuksi olisi hyvä varata aikaa perusteelliselle keskustelulle ja ratkaisuehdotuksille, sillä on tärkeää, että oppilaat oppivat asioita niin, että opiskeltu asia kytkeytyy lapsen ajatteluun ja oppimiseen, mutta samalla syrjäyttäen virheelliset käsitykset aiheesta, joita saattaa muodostua tutkivan lähestymistavan kautta. Tämän vuoksi on tärkeää tunnistaa ja ennaltaehkäistä mahdollisia virhekäsityksiä perusteellisen jälkipuinnin kautta. Kaiken kaikkiaan uskon, että tutkiva ja ilmiöpohjainen lähestymistapa on oiva keino tutkia Hanoin tornin mysteeriä oppilaiden kanssa.

Hanoin tornia voi virtuaalisesti tutkia esimerkiksi tästä linkistä.