Teksti: Milja Niemi, Venla Väli-Torola & Miia Liimatainen Kuvat: Saara Lehto
Königsbergin siltaongelma
Königsbergin eli nykyisen Kaliningradin läpi virtaa Pregolja-joki, jonka keskellä on kaksi saarta. Saaria yhdisti 1700-luvulla 7 siltaa. Sveitsiläinen matemaatikko Leonhard Euler keksi noihin aikoihin Königsbergin siltaongelman.
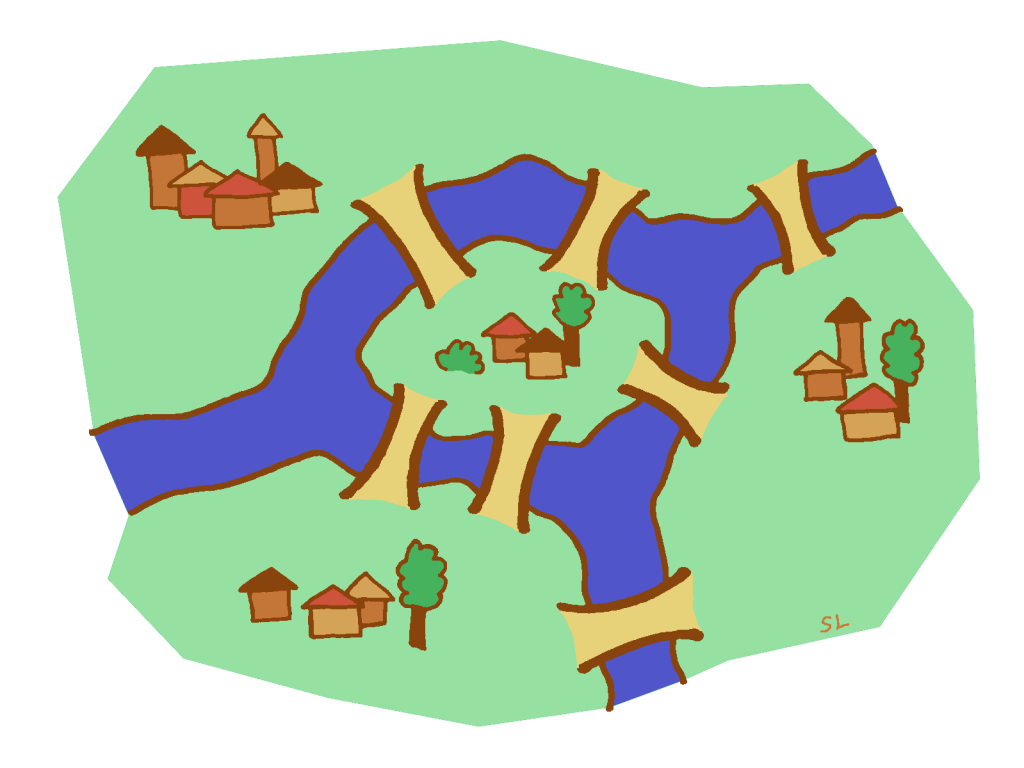
Ongelmana on keksiä sellainen reitti, jota kulkemalla voitaisiin ylittää jokainen silta täsmälleen yhden kerran. Reitin voi aloittaa mistä kohtaa vain maalta ja lopettaa myös mihin kohtaan vain. Ei tarvitse siis päätyä aloituspisteeseen. Löytyykö tällaista reittiä?
Alla on esitetty Königsbergin lisäksi kolme muutakin karttaa. Millä kartoilla reittiongelmaan löytyy ratkaisu? Millä kartoilla reittiä ei tunnu löytyvän?
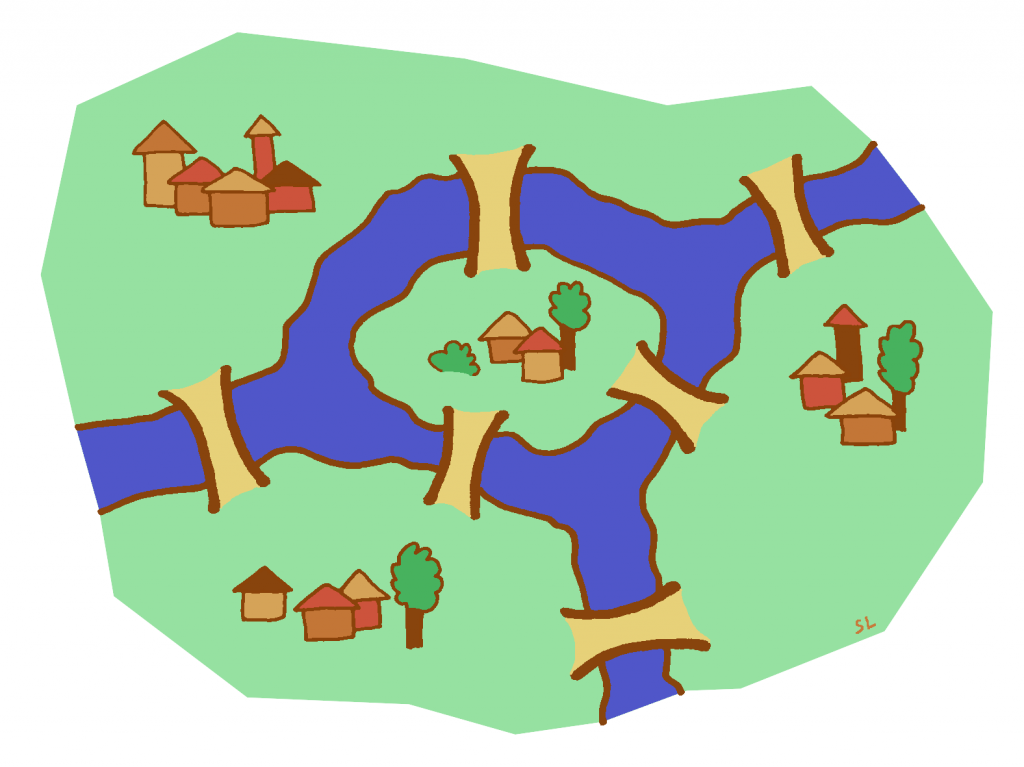
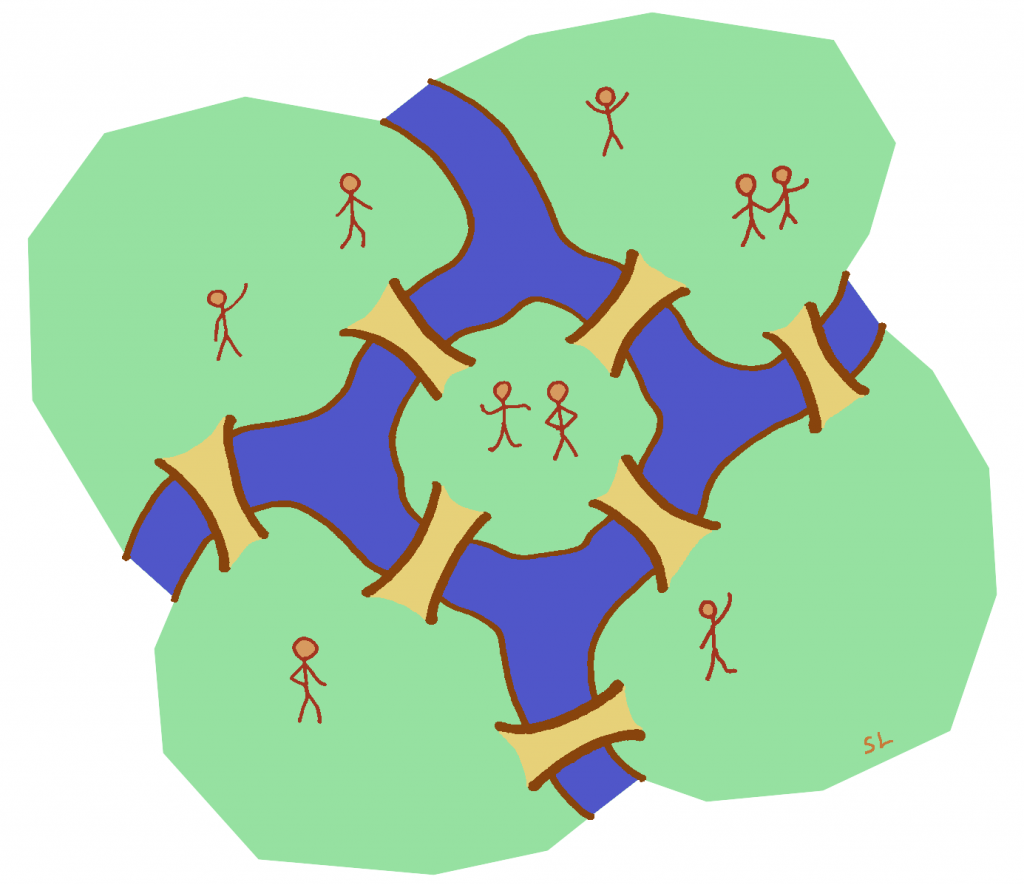
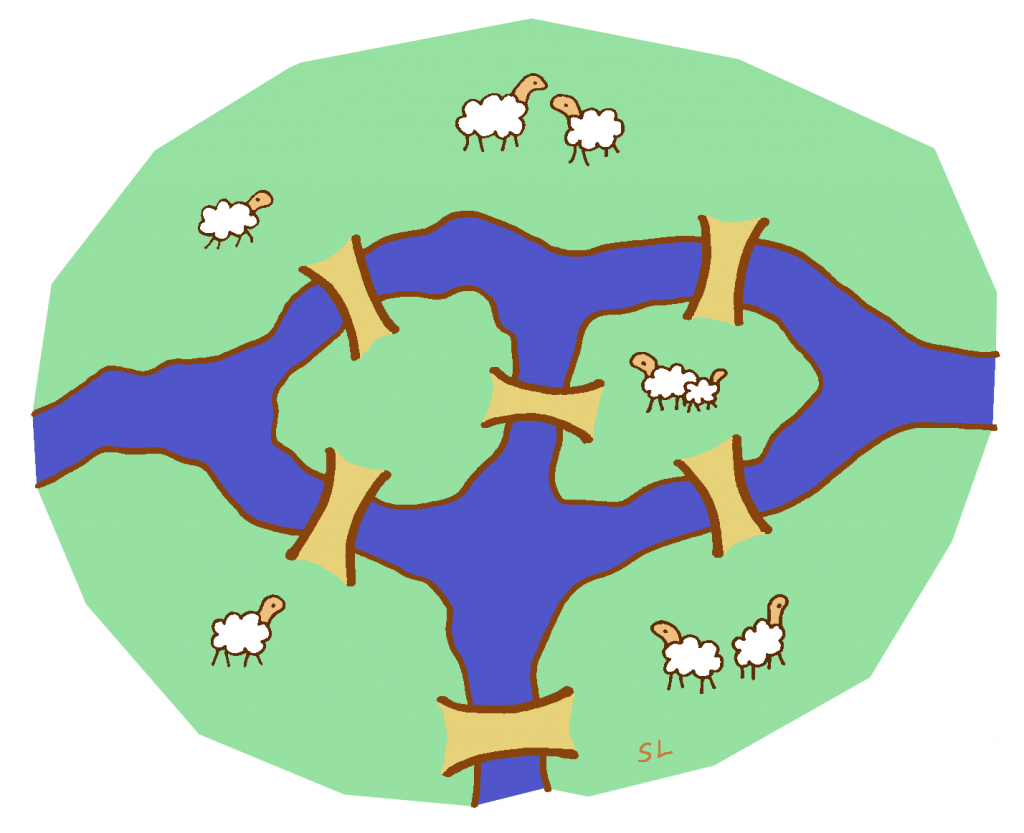
Löydätkö yhtäläisyyksiä niiden karttojen välillä joilta reitti löytyy tai niiden karttojen välillä joilta reittiä ei löydy?
Tarkastele karttoja joissa reittiä ei löydy. Auttaisiko jos joen yli rakennettaisiin johonkin kohtaan uusi silta?
Verkkoja, solmuja ja polkuja
Kun olet etsinyt reittejä eri kartoilta riittämiin, katsotaan, miten saadaan selville mitkä kartoista ovat ratkaistavissa. Tehdään kartoista uudet piirrokset, joissa maaosuudet on merkitty solmuilla (eli piirroksissa ympyröinä) ja niitä yhdistävät sillat on merkitty poluilla (eli piirroksessa ympyröiden välisinä viivoina). Tällaista karttaa kutsutaan verkoksi. Alla on esimerkki kartasta 1 laaditusta verkosta.
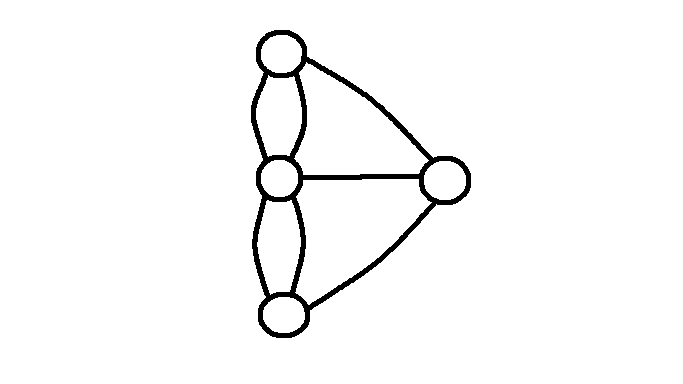
Ota verkosta 1 mallia ja piirrä vastaavat verkot muistakin kartoista.
Laske seuraavaksi, kuinka monta polkua (eli piirroksen viivaa) menee yhteen solmuun (eli ympyrään) ja kirjoita vastaus kunkin ympyrän sisälle. Verkossa 1 luvut näyttävät siis tältä:
Laske polkujen määriä kuvaavat numerot myös muihin piirtämiisi verkkoihin.
Mitkä verkoista olivat mielestäsi ratkaistavissa? Löydätkö jotain erityistä solmujen numeroista niissä verkoissa, joista ratkaisu löytyi? Onko väliä mistä solmusta aloitat ja mihin lopetat? Mitä yhteistä on verkoilla, joita et saanut ratkaistua? Millaisen säännön voisimme keksiä sille, milloin verkko voidaan ratkaista? Jos reittiä ei löydy, millaisia solmuja on paljon?
Vinkki: Voit googlata apua hakusanoilla ”Eulerin polku”.
Ratkaisut voit tarkistaa täältä!
Tällaista matematiikkaa kutsutaan verkkoteoriaksi. Jos kiinostuit, voit käydä tutkimassa lisää ongelmia Mathigonin sivuilla (englanniksi): https://mathigon.org/course/graph-theory/bridges
Voit myös katsoa suomenkielisiä verkkotehtäviä Summamutikan materiaalipankista: