Teksti ja kuvat: Alisa Uusi-Kilponen
Luokkataso: 7.-9.lk
Tarvittavat välineet: teippiä, mittanauha tai narua ja viivoitin, laskin, kynää ja paperia
Kuvaus: Etsitään ympäriltä löytyvistä ja itse luoduista nurkista erisuuruisia kulmia. Merkitään kulmiin kateetit teipillä. Mitataan mittanauhalla tai viivoittimella kateettien pituudet. Mitataan myös kateettien päätepisteiden väliin muodostuvan hypotenuusan pituus suoraan mittanauhalla tai vaihtoehtoisesti langalla ja viivoittimella. Todistetaan Pythagoraan lauseen avulla kulman olevan suora tai epäsuora.
Tehtävään menevä aika: noin 45 minuuttia (kun Pythagoraan lause on entuudestaan tuttu)
Johdattelu: Pythagoraan lauseen mieleen palauttaminen
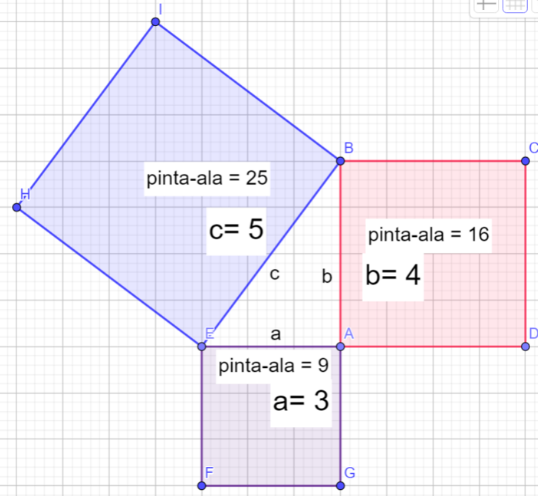
Suorakulmaisen kolmion kateettien a ja b neliöiden summa on hypotenuusan c neliö: a² + b² = c²
Siis esimerkkikuvan kolmio on suorakulmainen, sillä
3² + 4² = 5² on sama kuin
9 + 16 = 25 eli yhtälön molemmat puolet ovat selvästi yhtä suuret.
Pythagoraan lauseellahan saimme mm.
- todistettua sen, onko kolmio suorakulmainen (kolmio on silloin suorakulmainen, kun yhtälö pätee)
- selvitettyä hypotenuusan pituus, kun kateettien pituudet tunnetaan
- selvitettyä toisen kateetin pituus, kun toisen kateetin ja hypotenuusan pituudet tunnetaan
Mutta mitä hyötyä lauseesta on todellisuudessa? Kaavan ulkoa opettelun sijaan on hyvä ymmärtää se, mitä kaikkea se mahdollistaakaan.
Pythagoraan lauseen avulla saattaa olla helpompi suunnistaa jopa monien yllättävienkin arjen ongelmatilanteidenkin läpi. Myös etenkin arkkitehtuurissa ja rakennusmailla kyseistä lausetta hyödynnetään paljon, kuten seuraava video havainnollistaa: https://www.youtube.com/watch?v=r74qFUiZ2LE
Varmistamalla rakenteiden suoruus Pythagoraan lauseen avulla, varmistetaan niiden luotettavuus. Hyppää ammattilaisten saappaisiin, ja lähde itsekin tutkimaan erilaisia kulmia ja niiden suoruutta.
Toiminta: todistetusti suora vai epäsuora kulma?
Etsi ympäriltäsi vähintään kaksi erilaista kulmaa, kuten lattian ja huonekalun väliin jäävää tai vaakatasossa joidenkin seinämien väliin muodostuvaa nurkkaa. Yritä näiden kahden valmiiksi löytämäsi kulman lisäksi luoda itse ainakin yksi suorakulmainen kolmio saatavilla olevista materiaaleistasi. Yksi mahdollinen esimerkki on muodostaa kolmio kahdesta kirjasta asettaen niiden selkämykset kateeteiksi. Käytä luovuuttasi hyödyksi!
Mieti sitten, miten tarkistaisit esimerkiksi sen, ovatko seinäsi täysin suorat, miksi tuolin jalka on lattiaan nähden hieman epäsuorassa kulmassa tai onnistuitko asettamaan omatekemäsi suorakulmaisen kolmion oikeasti 90 asteen kulmaan, vaikka silmämääräisesti se siltä näyttääkin? Mietittyäsi erilaisia keinoja, miten saisit todistettua kulmiesi suoruuden tai epäsuoruuden, aloita todistaminen.
Todistamisessa voit hyödyntää tai soveltaa videolla nähtyä tai seuraavaa esimerkkiä:
- Merkitsen etsimästäni kulmasta haluamani mittaiset kateetit teipillä. Mittaan mittanauhalla tai viivoittimella kateettien pituudet senttimetreissä millimetrien tarkkuudella (5,0 cm) ja kirjaan tiedot ylös paperille, kuten alla.
Mittaan kateettien päätepisteiden väliin muodostuvan hypotenuusan pituuden senttimetreissä millimetrien tarkkuudella (7,3 cm). Mittaus onnistuu taipuvalla mittanauhalla tai langalla, jonka pituuden voin mitata viivoittimella.




Teen saamistani kateettien sekä hypotenuusan pituuksista Pythagoraan lauseen mukaisen yhtälön, jonka avulla todistan, onko kulmani suora vai epäsuora. Kirjaan ylös johtopäätökseni.
Toistan samat vaiheet toisellekin etsimälleni tai tekemälleni kulmalle.
Kulma 1: ___________________________
Kulman 1 kateettien pituudet: _________________________
Kulman 1 hypotenuusan pituus:________________________
Muodostuva Pythagoraan lauseen mukainen yhtälö ja sen ratkaisu:
Johtopäätökset.:_________________________
Yhteenveto:
Muista, että kaikki mittaustulokset ovat likiarvoja, joten pienen pienet erot yhtäsuuruudessa voivat olla mittaustarkkuudesta johtuvia. Silminnähden suoran näköiset kulmat eivät kuitenkaan riitä matemaattisiksi todisteiksi. Tarvitaan johdettavissa olevia Pythagoraan lauseen kaltaisia lauseita, joita hyödyntämällä voidaan todistaa väitteitä matemaattisesti todeksi. Oleellistahan rakennusmaillakin on, että seinät tai muut rakennelmat tulevat todellakin suoriksi.
Tehtävän esimerkkikuvista löytyvä tuolin jalan ja lattian väliin muodostuva kulmakin voi näyttää suoralta olematta kuitenkaan sitä. Osaatko esimerkkikuvien tietojen perusteella laskea, mikä on toisen kateetin pituus? Onko kyseinen tuolin jalan ja lattian väliin muodostuva kulma suora vai ei?
Jos geometria innostaa, voit tutustua myös toiseen yläkoulun geometrian tehtävään jossa tutkitaan ympyröitä:
https://blogs.helsinki.fi/summamutikka/ympyrageometriaa/
Kaikki geometriaan liittyvät Summamutikan materiaalipankin tehtävät:
https://blogs.helsinki.fi/summamutikka/?s=geometria